Baccalauréat S Amérique du Sud 24 novembre 2015 - Correction Exercice 1

Page 2 sur 10: Correction Exercice 1

Correction de l'exercice 1 (5 points)

Commun à tous les candidats

 

Partie A

Dans le plan muni d'un repère orthonormé $(,O;\vec{i},\vec{j} \,)$ on désigne par $\mathcal{C}_u$ la courbe représentative de la fonction $u$ définie sur l'intervalle $]0;+ \infty[$ par : \[u(x) = a + \dfrac{b}{x} + \dfrac{c}{x^2}\] où $a, b$ et $c$ sont des réels fixés. On a tracé sur le graphique ci-dessous la courbe $\mathcal{C}_u$ et la droite $\mathcal{D}$ d'équation $y = 1$.

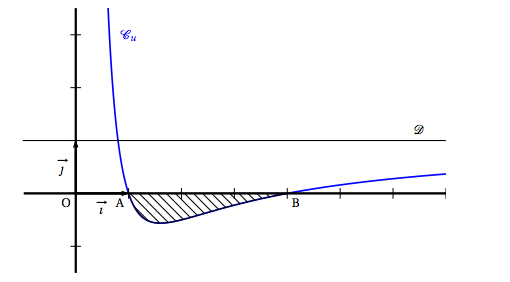
On précise que la courbe $\mathcal{C}_u$ passe par les points A(1;0) et B(4;0) et que l'axe des ordonnées et la droite $\mathcal{D}$ sont asymptotes à la courbe $\mathcal{C}_u$.

1. Donner les valeurs de $u(1)$ et $u(4)$.
La courbe $\mathscr{C}_u$ passe par $A(1;0)$ par conséquent $u(1)=0$.
Elle passe également pas $B(4;0)$ donc $u(4)=0$.
$\quad$
2. Donner $\displaystyle\lim_{x \to + \infty} u(x)$. En déduire la valeur de $a$.
$\lim\limits_{x\to +\infty} \dfrac{1}{x}=0$ et $\lim\limits_{x\to +\infty} \dfrac{1}{x^2}=0$.
Donc $\lim\limits_{x\to +\infty} u(x)=a$.
La droite d’équation $y=1$ étant asymptote à la courbe $\mathscr{C}_u$ cela signifie donc que $a=1$.
$\quad$
3. En déduire que, pour tout réel $x$ strictement positif, $u(x) = \dfrac{x^2 - 5x + 4}{x^2}$.
Ainsi $u(x)=1+\dfrac{b}{x}+\dfrac{c}{x^2}$.
Puisque $u(1)=0$ on obtient $1+b+c=0$ soit $b+c=-1 \quad (1)$.
Puisque $u(4)=0$ on obtient $1+\dfrac{b}{4}+\dfrac{c}{16}=0$ soit $16+4b+c=0$ ou encore $4b+c=-16 \quad (2)$.
On fait $(2)-(1)$ : $3b=-15$ soit $b=-5$
Ainsi $-5+c=-1$ soit $c=4$.
On vérifie dans l’équation $2$ $4\times (-5)+4=-20+4=-16$
$\quad$
Par conséquent $u(x)=1-\dfrac{5}{x}+\dfrac{4}{x^2} = \dfrac{x^2-5x+4}{x^2}$.
$\quad$

 

Partie B

Soit $f$ la fonction définie sur l'intervalle $]0;+ \infty[$ par : \[f(x) = x - 5\ln x - \dfrac{4}{x}.\]

1. Déterminer la limite de $f(x)$ lorsque $x$ tend vers $0$. On pourra utiliser sans démonstration le fait que $\displaystyle\lim_{x \to 0} x \ln x = 0$.
$f(x)=\dfrac{x^2-5x\ln x-4}{x}$.
$\lim\limits_{x \to 0^+} x\ln x=0$ donc $\lim\limits_{x \to 0^+}x^2-5x\ln x-4 = -4$
Or $\lim\limits_{x \to 0^+} x=0^+$
Par conséquent $\lim\limits_{x \to 0^+} f(x)=-\infty$.
$\quad$
2. Déterminer la limite de $f(x)$ lorsque $x$ tend vers $+ \infty$.
$f(x)=x\left(1-\dfrac{\ln x}{x}-\dfrac{4}{x^2}\right)$.
$\lim\limits_{x \to +\infty} \dfrac{\ln x}{x}=0$ et $\lim\limits_{x \to +\infty} \dfrac{1}{x^2}=0$.
Donc $\lim\limits_{x \to +\infty} \left(1-\dfrac{\ln x}{x}-\dfrac{4}{x^2}\right) =1$ et $\lim\limits_{x \to +\infty} f(x)=+\infty$.
$\quad$
3. Démontrer que, pour tout réel $x$ strictement positif, $f'(x) = u(x)$. En déduire le tableau de variation de la fonction $f$ en précisant les limites et les valeurs particulières.
La fonction $f$ est dérivable sur $]0;+\infty[$ comme somme de fonctions dérivables sur cet intervalle.
$f'(x)=1-5\times \dfrac{1}{x}+\dfrac{4}{x^2} = u(x)$.
Le signe de $u(x)$ ne dépend que de celui de $x^2-5x+4=(x-1)(x-4)$
On obtient ainsi le tableau de variations suivant :

 

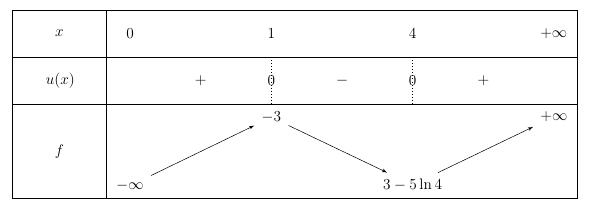
Partie C

 

1. Déterminer l'aire $\mathcal{A}$, exprimée en unité d'aire, du domaine hachuré sur le graphique de la \textbf{partie A}.
L’aire hachurée correspond à l’aire du domaine situé entre l’axe des abscisses, la courbe $\mathscr{C}_u$ et les droites d’équation $x=0$ et $x=4$.
La fonction $-u$ est continue et positive sur $[1;4]$.
Ainsi :
$\begin{align*} \mathscr{A}&=\int_1^4-u(x)\mathrm{d}x\phantom{\dfrac{1}{4}} \\\\
&=-\left(f(4)-f(1)\right) \\\\
&=-(3-5\ln 4 +3) \\\\
&=5\ln 4-6
\end{align*}$
$\quad$
2. Pour tout réel $\lambda$ supérieur ou égal à 4, on note $\mathcal{A}_{\lambda}$ l'aire, exprimée en unité d'aire, du domaine formé par les points $M$ de coordonnées $(x;y)$ telles que \[4 \leqslant x \leqslant \lambda\quad \text{et}\quad 0 \leqslant y \leqslant u(x).\] Existe-t-il une valeur de $\lambda$ pour laquelle $\mathcal{A}_{\lambda} = \mathcal{A}$ ? Dans cette question, toute trace de recherche, même incomplète, ou d'initiative, même non fructueuse, sera prise en compte dans l'évaluation.
L’aire $\mathscr{A}_{\lambda}$ correspond à l’aire du domaine situé entre la courbe $\mathscr{C}_u$, l’axe des abscisses et les droites d’équation $x=4$ et $x=\lambda$.
La fonction $u$ est continue et positive sur $[4;\lambda]$.
Ainsi :
$\begin{align*} \mathscr{A}_{\lambda}&=\int_4^{\lambda}u(x)\mathrm{d}x\phantom{\dfrac{1}{4}} \\\\
&=f(\lambda)-f(4) \\\\
&=f(\lambda)-\left(3-5\ln 4\right) \\\\
&=f(\lambda)-\dfrac{4}{\lambda}-3+5\ln 4
\end{align*}$
On veut donc résoudre l’équation $f(\lambda)-3+5\ln 4=5\ln 4 -6$
soit $f(\lambda)=-3$.
La fonction $f$ est continue (car dérivable) et strictement croissante sur $[4;+\infty[$.
De plus $f(4)=3-5\ln 4 <-3$ et $\lim\limits_{x \to +\infty} f(x)=+\infty$
Par conséquent $-3\in [f(4);+\infty[$.
D’après le théorème de la bijection (ou corollaire du théorème des valeurs intermédiaires), l’équation $f(\lambda)=-3$ possède une unique solution.
$\quad$
Il existe donc une valeur de $\lambda$ telle que $\mathscr{A}=\mathscr{A}_{\lambda}$
$\quad$