Baccalauréat S Amérique du Sud 24 novembre 2015 - Correction Exercice 3

Page 6 sur 10: Correction Exercice 3

Correction de l'exercice 3 (5 points)

Commun à tous les candidats

Les trois parties A, B et C peuvent être traitées de façon indépendante

Partie A

Le chikungunya est une maladie virale transmise d'un être humain à l'autre par les piqûres de moustiques femelles infectées.
Un test a été mis au point pour le dépistage de ce virus. Le laboratoire fabriquant ce test fournit les caractéristiques suivantes :

• la probabilité qu'une personne atteinte par le virus ait un test positif est de $0,98$ ;
• la probabilité qu'une personne non atteinte par le virus ait un test positif est de $0,01$.

On procède à un test de dépistage systématique dans une population «cible ». Un individu est choisi au hasard dans cette population. On appelle :

• $M$ l'évènement: «L'individu choisi est atteint du chikungunya »
• $T$ l'évènement: «Le test de l'individu choisi est positif »

On notera $\overline{M}$ (respectivement $\overline{T}$) l'évènement contraire de l'évènement $M$ (respectivement $T$). On note $p\: (0 \leqslant p \leqslant 1$) la proportion de personnes atteintes par la maladie dans la population cible.

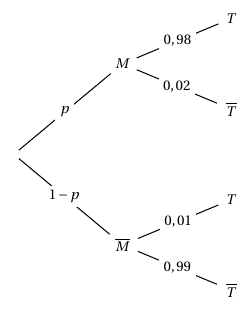
1. 1. Recopier et compléter l'arbre de probabilité ci-dessous.
   
   
   2. Exprimer $P(M \cap T),\: P\left(\overline{M} \cap T\right)$ puis $P(T)$ en fonction de $p$.
   $P(M\cap T) = 0,98p$ $\quad$ $P\left(\overline{M} \cap T\right) = 0,01(1-p)$
   D’après la formule des probabilités totales on a :
   $\begin{align*} P(T) &= P(M \cap T) + P\left(\overline{M} \cap T\right) \\\\
   &= 0,98p + 0,01(1-p) \\\\
   &=0,98p +0,01-0,01p\\\\
   &=0,97p+0,01
   \end{align*}$
2. 1. Démontrer que la probabilité de $M$ sachant $T$ est donnée par la fonction $f$ définie sur [0 ; 1] par : \[f(p) = \dfrac{98p}{97p+1}.\]
   On veut calculer
   $P_T(M)=\dfrac{P(M\cap T)}{P(T)}$ $ = \dfrac{0,98p}{0,97p+0,01} = \dfrac{98p}{97p+1}$
   $\quad$
   
   2. Étudier les variations de la fonction $f$.
   La fonction $f$ est dérivable sur $[0;1]$ en tant que quotient de fonctions dérivables dont le dénominateur ne s’annule pas sur $[0;1]$
   $f'(p)=\dfrac{98(97p+1)-97\times 98p}{(97p+1)^2} = \dfrac{98}{(97p+1)^2} >0$.
   La fonction $f$ est donc strictement croissante sur $[0;1]$.
3. On considère que le test est fiable lorsque la probabilité qu'une personne ayant un test positif soit réellement atteinte du chikungunya est supérieure à $0,95$. En utilisant les résultats de la question \textbf{2.}, à partir de quelle proportion $p$ de malades dans la population le test est-il fiable ?
On veut résoudre l’inéquation :
$\begin{align*} f(p)> 0,95 &\Leftrightarrow \dfrac{98p}{97p+1} > 0,95 \\\\
&\Leftrightarrow 98p > 0,95(97p+1) \\\\
&\Leftrightarrow 98p>92,15p+0,95 \\\\
&\Leftrightarrow 5,85p>0,95 \\\\
&\Leftrightarrow p>\dfrac{0,95}{5,85} \\\\
&\Leftrightarrow p>\dfrac{19}{117}
\end{align*}$

 

Partie B

En juillet 2014, l'institut de veille sanitaire d'une île, en s'appuyant sur les données remontées par les médecins, publie que 15 % de la population est atteinte par le virus. Comme certaines personnes ne consultent pas forcément leur médecin, on pense que la proportion est en réalité plus importante. Pour s'en assurer, on se propose d'étudier un échantillon de 1000 personnes choisies au hasard dans cette île. La population est suffisamment importante pour considérer qu'un tel échantillon résulte de tirages avec remise. On désigne par $X$ la variable aléatoire qui, à tout échantillon de 1000 personnes choisies au hasard, fait correspondre le nombre de personnes atteintes par le virus et par $F$ la variable aléatoire donnant la fréquence associée.

1. 1. Sous l'hypothèse $p = 0,15$, déterminer la loi de $X$.
   Les $1~000$ tirages sont indépendants, aléatoires avec remises et présentent chacun deux issues : $M$ et $\overline{M}$.
   De plus $P(M)=0,15$.
   $X$ suit donc la loi binomiale de paramètres $n=1~000$ et $p=0,15$.
   
   2. Dans un échantillon de 1000 personnes choisies au hasard dans l'île, on dénombre $197$ personnes atteintes par le virus. Quelle conclusion peut-on tirer de cette observation à propos du chiffre de 15 % publié par l'institut de veille sanitaire ? Justifier. (On pourra s'aider du calcul d'un intervalle de fluctuation au seuil de 95 %.)
   $n=1~000$ et $p=0,15$
   $n=1~000 \ge 30 \checkmark$ $\quad$ $np=150 \ge 5 \checkmark$ $\quad$ $n(1-p)=850 \ge 5 \checkmark$.
   Un intervalle de fluctuation asymptotique au seuil de $95\%$ est alors :
   $\begin{align*} I_{1~000} &= \left[0,15-1,96\sqrt{\dfrac{0,15 \times 0,85}{1~000}};0,15+ 1,96\sqrt{\dfrac{0,15 \times 0,85}{1~000}}\right] \\\\
   &\approx [0,127;0,173]
   \end{align*}$
   La fréquence observée est $f=\dfrac{197}{1~000} = 0,197 \notin I_{1~000}$
   On peut donc remettre en cause le chiffre publié par l’institut de veille sanitaire.
   $\quad$
2. On considère désormais que la valeur de $p$ est inconnue. En utilisant l'échantillon de la question 1. b. , proposer un intervalle de confiance de la valeur de $p$, au niveau de confiance de 95 %.
$n=1~000 \ge 30 \checkmark$ $\quad$ $nf=197 \ge 5 \checkmark$ $\quad$ $n(1-f)=803 \ge 5 \checkmark$.
Un intervalle de confiance au seuil de confiance de $95\%$ est :
$\begin{align*} J_{1~000}&=\left[0,197-\dfrac{1}{\sqrt{1~000}};0,197+\dfrac{1}{\sqrt{1~000}}\right] \\\\
&\approx [0,165;0,229]
\end{align*}$

 

Partie C

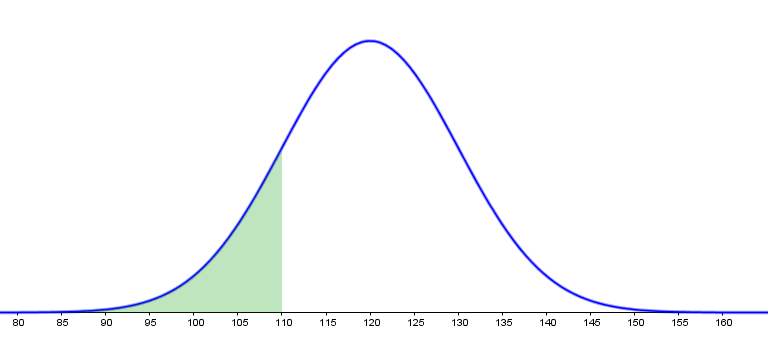
Le temps d'incubation, exprimé en heures, du virus peut être modélisé par une variable aléatoire $T$ suivant une loi normale d'écart type $\sigma = 10$. On souhaite déterminer sa moyenne $\mu$. La représentation graphique de la fonction densité de probabilité de $T$ est donnée en annexe.

1. 1. Conjecturer, à l'aide du graphique, une valeur approchée de $\mu$.
   D’après le graphique, on peut conjecturer que $\mu \approx 120$.
   
   2. On donne $p(T < 110) = 0,18$. Hachurer sur le graphique un domaine dont l'aire correspond à la probabilité donnée.
   
2. On note $T'$ la variable aléatoire égale à $\dfrac{T - \mu}{10}$.
   1. Quelle loi la variable aléatoire $T'$ suit-elle ?
   $T’$ suit la loi normale centrée réduite.
   $\quad$
   
   2. Déterminer une valeur approchée à l'unité près de la moyenne $\mu$ de la variable aléatoire $T$ et vérifier la conjecture de la question 1.
   $\begin{align*} p(T<110)=0,18 &\Leftrightarrow p(T-\mu<110-\mu)=0,18 \\\\
   &\Leftrightarrow p\left(\dfrac{T-\mu}{10}<\dfrac{110-\mu}{10}\right) = 0,18 \\\\
   &\Leftrightarrow p\left(T'<\dfrac{110-\mu}{10}\right) = 0,18
   \end{align*}$
   En utilisant la calculatrice, on trouve que $\dfrac{110-\mu}{10}\approx -0,915$ soit $\mu \approx 119$.
   Cette valeur est très proche de celle conjecturée à la question 1. $\quad$