Baccalauréat S Nouvelle-Calédonie 19 novembre 2015
Exercice 1 7 points
Une usine produit de l'eau minérale en bouteilles. Lorsque le taux de calcium dans une bouteille est inférieur à 6,5 mg par litre, on dit que l'eau de cette bouteille est très peu calcaire.
Dans cet exercice les résultats approchés seront arrondis au millième.
Partie A
L'eau minérale provient de deux sources, notées «source A » et «source B ». La probabilité que l'eau d'une bouteille prélevée au hasard dans la production d'une journée de la source A soit très peu calcaire est $0,17$. La probabilité que l'eau d'une bouteille prélevée au hasard dans la production d'une journée de la source B soit très peu calcaire est $0,10$.
La source A fournit 70% de la production quotidienne totale des bouteilles d'eau et la source B le reste de cette production.
On prélève au hasard une bouteille d'eau dans la production totale de la journée. On considère les évènements suivants : $A$ :«La bouteille d'eau provient de la source A » $B$ :«La bouteille d'eau provient de la source B » $S$ :«L'eau contenue dans la bouteille d'eau est très peu calcaire ».
- Déterminer la probabilité de l'évènement $A \cap S$.
- Montrer que la probabilité de l'évènement $S$ vaut $0,149$.
- Calculer la probabilité que l'eau contenue dans une bouteille provienne de la source A sachant qu'elle est très peu calcaire.
- Le lendemain d'une forte pluie, l'usine prélève un échantillon de 1000 bouteilles provenant de la source A. Parmi ces bouteilles, $211$ contiennent de l'eau très peu calcaire. Donner un intervalle permettant d'estimer au seuil de 95 % la proportion de bouteilles contenant de l'eau très peu calcaire sur l'ensemble de la production de la source A après cette intempérie.
Partie B
On note $X$ la variable aléatoire qui, à chaque bouteille prélevée au hasard dans la production d'une journée de la source A, associe le taux de calcium de l'eau qu'elle contient. On suppose que $X$ suit la loi normale de moyenne $8$ et d'écart-type $1,6$. On note $Y$ la variable aléatoire qui, à chaque bouteille prélevée au hasard dans la production d'une journée de la source B, associe le taux de calcium qu'elle contient. On suppose que $Y$ suit la loi normale de moyenne $9$ et d'écart-type $\sigma$.
- Déterminer la probabilité pour que le taux de calcium mesuré dans une bouteille prise au hasard dans la production d'une journée de la source A soit compris entre $6,4$ mg et $9,6$ mg.
- Calculer la probabilité $p(X \leqslant 6,5)$.
- Déterminer $\sigma$ sachant que la probabilité qu'une bouteille prélevée au hasard dans la production d'une journée de la source B contienne de l'eau très peu calcaire est $0,1$.
Partie C
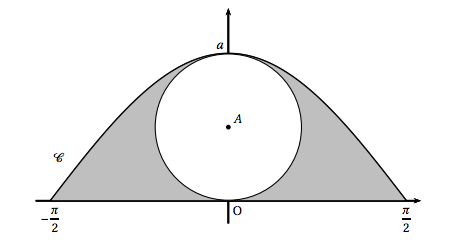
Le service commercial a adopté pour les étiquettes des bouteilles la forme représentée ci-dessous dans un repère orthonormé du plan. La forme de ces étiquettes est délimitée par l'axe des abscisses et la courbe $\mathcal{C}$ d'équation $y = a\cos x$ avec $x \in \left[- \frac{\pi}{2}~;~\frac{\pi}{2}\right]$ et $a$ un réel strictement positif.
Un disque situé à l'intérieur est destiné à recevoir les informations données aux acheteurs. On considère le disque de centre le point A de coordonnées $\left(0~;~\frac{a}{2}\right)$ et de rayon $\frac{a}{2}$. On admettra que ce disque se trouve entièrement en dessous de la courbe $\mathcal{C}$ pour des valeurs de $a$ inférieures à $1,4$.
- Justifier que l'aire du domaine compris entre l'axe des abscisses, les droites d'équation $x = - \frac{\pi}{2}$ et $x = \frac{\pi}{2}$, et la courbe $\mathcal{C}$ est égale à $2a$ unités d'aire.
- Pour des raisons esthétiques, on souhaite que l'aire du disque soit égale à l'aire de la surface grisée. Quelle valeur faut-il donner au réel $a$ pour respecter cette contrainte ?
- Vues: 38032
