Baccalauréat S Liban 29 mai 2018 - Correction Exercice 5
Page 10 sur 12
Correction de l'exercice 5 5 points
Un jeu de hasard sur ordinateur est paramétré de la façon suivante :
- Si le joueur gagne une partie, la probabilité qu'il gagne la partie suivante est $\dfrac{1}{4}$ ;
- Si le joueur perd une partie, la probabilité qu'il perde la partie suivante est $\dfrac{1}{2}$ ;
- La probabilité de gagner la première partie est $\dfrac{1}{4}$ .
Pour tout entier naturel $n$ non nul, on note $G_n$ l'évènement " la $n^\text{e}$ partie est gagnée " et on note $p_n$ la probabilité de cet évènement. On a donc $p_1 = \dfrac{1}{4}$.
- Montrer que $p_2 = \dfrac{7}{16}$. On utilise l'arbre pondéré ci-dessous :
- Montrer que, pour tout entier naturel $n$ non nul, $p_{n+1} = - \dfrac{1}{4}p_n + \dfrac{1}{2}$. On utilise l'arbre pondéré ci-dessous :
- On obtient ainsi les premières valeurs de $p_n$ : $$\begin{array} {|c|c|c|c|c|c|c|c|}\hline n &1 &2 &3 &4 &5 &6 &7\\ \hline p_n & 1 & 0,4375 & 0,3906 & 0,4023 & 0,3994 & 0,4001 & 0,3999 \\ \hline \end{array}$$ Quelle conjecture peut -on émettre ? Il semblerait que la limite de la suite $\left(p_n\right)$ soit $0,4$.
- On définit, pour tout entier naturel $n$ non nul, la suite $\left(u_n\right)$ par $u_n = p_n - \dfrac{2}{5}$.
- Démontrer que la suite $\left(u_n\right)$ est une suite géométrique dont on précisera la raison. Pour tout entier naturel $n$ non nul on a $u_n=p_n-\dfrac{2}{5}$ soit $p_n=u_n+\dfrac{2}{5}$.
- En déduire que, pour tout entier naturel $n$ non nul, $p_n = \dfrac{2}{5} - \dfrac{3}{20}\left(- \dfrac{1}{4}\right)^{n-1}$. Ainsi, pour tout entier naturel $n$ non nul, on a $u_n=-\dfrac{3}{20}\left(-\dfrac{1}{4}\right)^{n-1}$.
- La suite $\left(p_n\right)$ converge-t-elle ? Interpréter ce résultat. On a $-1<-\dfrac{1}{4}<1$ donc $\lim\limits_{n \to +\infty} \left(-\dfrac{1}{4}\right)^{n-1}=0$.
$\begin{align*} u_{n+1}&=p_{n+1}-\dfrac{2}{5} \\
&=-\dfrac{1}{4}p_n+\dfrac{1}{2}-\dfrac{2}{5} \\
&=-\dfrac{1}{4}\left(u_n+\dfrac{2}{5}\right)+\dfrac{1}{10} \\
&=-\dfrac{1}{4}u_n-\dfrac{1}{10}+\dfrac{1}{10} \\
&=-\dfrac{1}{4}u_n
\end{align*}$
La suite $\left(u_n\right)$ est donc géométrique de raison $-\dfrac{1}{4}$ et de premier terme $u_1=p_1-\dfrac{2}{5}=-\dfrac{3}{20}$.
$\quad$
Or $p_n=u_n+\dfrac{2}{5}=-\dfrac{3}{20}\left(-\dfrac{1}{4}\right)^{n-1}+\dfrac{2}{5}$.
$\quad$
Donc la suite $\left(p_n\right)$ converge vers $\dfrac{2}{5}=0,4$.
Sur le long terme, la probabilité qu’un joueur gagne une partie est $0,4$.
$\quad$
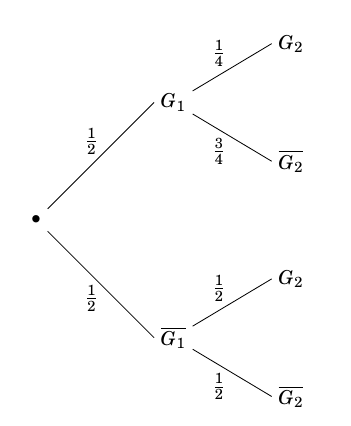
D’après la formule des probabilités totales on a :
$\begin{align*} p_2&=p\left(G_2\right) \\
&=p\left(G_1\cap G_2\right)+p\left(\overline{G_1}\cap G_2\right) \\
&=\dfrac{1}{4}\times \dfrac{1}{4}+\dfrac{3}{4}\times \dfrac{1}{2} \\
&=\dfrac{7}{16}
\end{align*}$
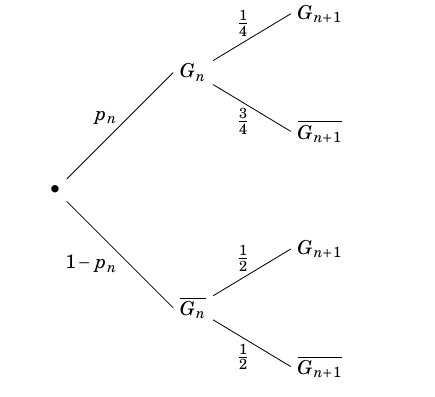
’après la formule des probabilités totales on a :
$\begin{align*} p_{n+1}&=p\left(G_{n+1}\right) \\
&=p\left(G_n\cap G_{n+1}\right)+p\left(\overline{G_n}\cap G_{n+1}\right) \\
&=\dfrac{1}{4}\times p_n+\dfrac{1}{2}\times \left(1-p_n\right) \\
&=\dfrac{p_n}{4}+\dfrac{1}{2}-\dfrac{p_n}{2} \\
&=-\dfrac{1}{4}p_n+\dfrac{1}{2}
\end{align*}$
$\quad$
- Vues: 24728
