Continuité

Page 1 sur 8

Continuité

Définition
Soit $f$ une fonction définie sur un intervalle $I$.
· Soit $a$ un réel appartenant à $I$.
            On dit que $f$ est continue en $a$ , si $\displaystyle\lim_{x \to a}f(x) = f(a)$.
· On dit que $f$ est continue sur $I$, si $f$ est continue en tout point $a$ de $I$.

Remarque

· Dire que $\displaystyle\lim_{x \to a}f(x) = f(a)$ revient aussi à dire que $\displaystyle\lim_{h \to 0}f(a + h) = f(a)$

 

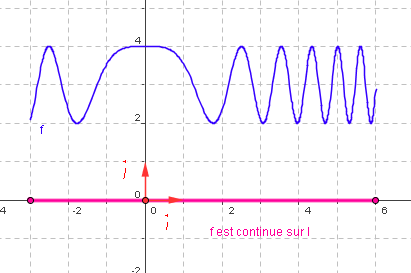
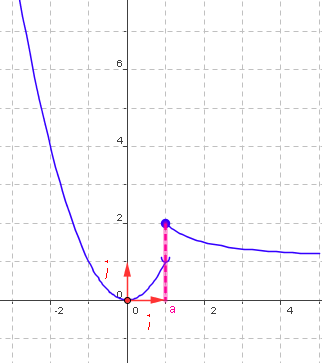
Graphiquement, on reconnaît qu'une fonction $f$ est continue sur $I$ lorsqu'on peut tracer sa courbe sur l'intervalle $I$ sans lever le stylo de la feuille.		Une fonction n'est pas continue en un point $a$ lorsque la courbe a une discontinuité en $a$, elle fait un "saut".
Fonction continue sur un intervalle :		Fonction discontinue en a

Exemple 1

· La fonction $x\mapsto x ^2$ est une fonction continue en tout point $a$ de $\mathbb{R}$ , elle est continue sur $\mathbb{R}$

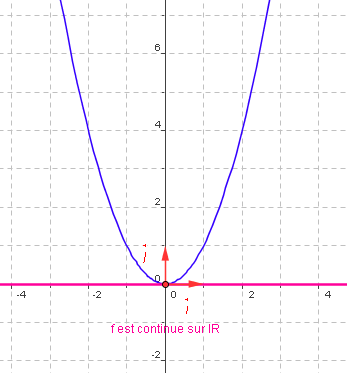
On peut le justifier en démontrant que$\displaystyle\lim_{x \to a} x ^2 = a^ 2$ , c'est-à-dire en démontrant que $x ^2$ est aussi proche que l'on veut de $a ^2 $ lorsqu'on prend $ x $ assez proche de $a$ .

La parabole représentant la fonction $x \mapsto x ^2$ peut être tracée sans lever le stylo de la feuille.