Continuité
Page 3 sur 8
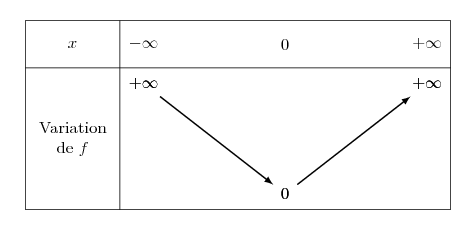
Convention
Il est convenu que, dans un tableau de variation de fonction, les flèches obliques indiquent que la fonction est continue et strictement monotone .
Exemple 3
Le tableau de variation de la fonction carré ( $f(x) = x^ 2$ ) signifie que la fonction carré est continue et strictement décroissante sur $]-\infty ; 0]$ et qu'elle est continue et strictement croissante sur $[0 ; +\infty[$
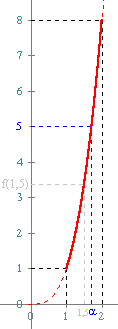
Théorème des valeurs intermédiaires Soit $f$ une fonction définie et continue sur un intervalle $I$.
Soient $a \in I$ et $b \in I$; pour tout réel $k$ compris entre $f(a)$ et $f(b) $ , il existe au moins un réel $c$ compris entre $a$ et $b$ tel que $f(c) = k $.
Soient $a \in I$ et $b \in I$; pour tout réel $k$ compris entre $f(a)$ et $f(b) $ , il existe au moins un réel $c$ compris entre $a$ et $b$ tel que $f(c) = k $.
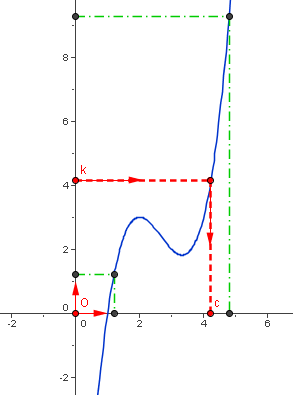
Ce que l'on peut aussi exprimer sous la forme : L'équation $f(x) = k$ a au moins une solution $c$ comprise entre $a$ et $b$ .
- Vues: 24615
