Continuité
Remarque
Ce théorème peut s'étendre à une fonction définie, continue et strictement monotone sur un intervalle ouvert éventuellement non borné en utilisant les limites de $f$ aux bornes de cet intervalle.
Par exemple :
· si $f$ est une fonction définie, continue et strictement décroissante sur $]-\infty ; a[ $ , alors pour tout réel $k$ dans l'intervalle $]\displaystyle\lim_{x \to + a^+};\displaystyle\lim_{x \to - \infty}f(x)[$ l'équation $f(x) = k$ a une solution unique dans$]-\infty ; a[$.
Exemple 5
La fonction $f$ définie par $f(x) = x^ 2$ est une fonction définie, continue et strictement croissante sur $[0 ; +\infty [$ .
On a $f (0) = 0$ et $ \displaystyle\lim_{x \to + \infty}f(x) = +\infty$ .
Pour tout réel $k \in [0 ; +\infty [$, l'équation $x ^ 2 = k$ a une solution unique dans $[0 ; +\infty [ $. Cette solution est $\sqrt{k}$
Donc $f $ réalise une bijection de $ [0 ; +\infty [$ sur $[0 ; +\infty [$ .
La fonction réciproque de la fonction "carré" est la fonction est la fonction "racine carrée".
Exemple 6
Démontrons que l'équation $\cos x =\dfrac{1}{4}$ une solution unique $\alpha$ dans $[0 ; \pi ]$ .
On connaît le tableau de variations de la fonction cosinus sur l'intervalle $[0 ; \pi ]$
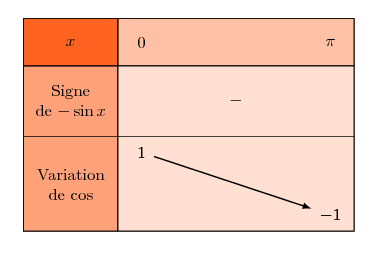
La fonction co\sinus est continue et strictement décroissante sur $[0 ; \pi ] $
On a $-1\leq \dfrac{1}{4}\leq 1$, ce tableau permet donc de justifier que l'équation $\cos x = \dfrac{1}{4}$ a , dans l'intervalle $ [0 ; \pi ]$ , une solution unique $\alpha$ .
On peut donner une valeur approchée de $\alpha$ par balayage de l'intervalle $[0 ; \pi ]$ par pas de 0,1
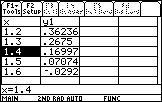
Une calculatrice ou un tableur peut donner les valeurs de $\cos x $ pour $x = 0,1 ; 0,2 ; 0,3$ etc...
|
|
On constate alors que $ \cos(1.4)\leq \dfrac{1}{4}\leq \cos(1.3)$
On peut en déduire que $1.3\leq \alpha\leq 1.4$ car la fonction cosinus est strictement décroissante sur $[0 ; \pi ]$.
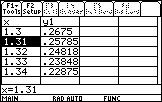
De même un balayage de l'intervalle $[ 1,3 ; 1,4 ]$ par pas de 0,01 permettra d'obtenir $1.31\leq \alpha\leq 1.32$
On en déduit que $a \approx 1,31$ à $10^{ -2}$ près par défaut.
Remarque
Les théorèmes précédents permettent de démontrer l'existence d'une ou de plusieurs solutions à une équation, mais il ne permettent pas de déterminer la valeur de ces solutions.
On pourra en donner des valeurs approchées en utilisant la méthode de dichotomie (exemple 4) ou la méthode de balayage (exemple 5).
- Vues: 24612
