Continuité
Exemple 4
$f$ définie par $f(x) = x^ 3$ est continue et strictement croissante sur $[0 ; +\infty[$ ,
$f (1) = 1$ et $f (2) = 8$
Donc pour tout $k \in [ 1 ; 8 ]$ , l'équation $x^ 3 = k$ a au moins une solution dans $[ 1 ; 2 ]$
En particulier l'équation $x ^3 = 5$ a au moins une solution $\alpha$ dans $[ 1 ; 2 ]$ .
De plus,$ f$ étant strictement croissante, si $x > \alpha$ , on a $f(x) > f ( \alpha )$, donc $x ^3 > 5$
et si $x < \alpha$ , on a $f(x) < f ( \alpha )$, donc $x ^3 < 5$ .
Il ne peut donc pas y avoir de solution à l'équation $x^ 3 = 5$, qui soit différente de $\alpha$ .
Donc l'équation $ x^ 3 = 5$ a une solution $\alpha$ unique dans l'intervalle $[ 1 ; 2 ]$ .
Déterminons une valeur approchée de $\alpha$ en utilisant la méthode de dichotomie.
On a $(1+2)/2=3/2=1,5$ ; $ f (1,5) =27/8< 5$ et $f (2) > 5$
Donc 5 est compris entre $f (1,5)$ et $f (2)$.
L'utilisation du théorème des valeurs intermédiaires permet alors d'affirmer que l'équation $x ^3 = 5$ a une solution comprise entre 1,5 et 2 .
Cette solution ne peut être que $\alpha$ . On a donc $1,5 < \alpha < 2$
On a $(1,5+2)/2= 1,75$ ; $f (1,75) = 5,359375$ donc $f (1,75) > 5$ et $f (1,5) < 5 $
Donc 5 est compris entre $f (1,5)$ et $f (1,75)$
L'utilisation du théorème des valeurs intermédiaires permet alors d'affirmer que l'équation $x ^3 = 5$ a une solution comprise entre 1,5 et 1,75 .
Cette solution ne peut être que $\alpha$ . On a donc $1,5 < \alpha < 1,75$
En réitérant le procédé, on obtient des encadrements de $\alpha$ d'amplitude diminuée de moitié à chaque étape.
Cela revient à dire que l'on construit deux suites $u_ n$ et $v_ n$ adjacentes dont la limite est $\alpha$ .
Après 4 étapes supplémentaires, on obtient $\alpha\approx 1,71$ à $10^{ -2}$ près .
Nota : ce réel $\alpha$ est appelé racine cubique de 5 , on note $\alpha =^3\sqrt{5} $
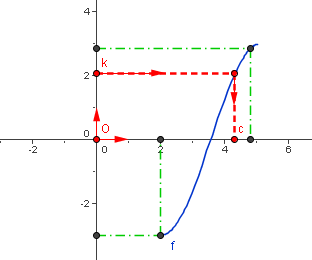
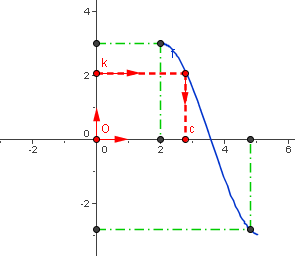
Pour tout réel $k$ compris entre $f(a)$ et $f(b)$ , il existe un et un seul réel $c$ dans $[a ; b]$ tel que $f(c) = k$.
Ce que l'on peut aussi exprimer sous la forme : L'équation $f(x) = k$ a une solution unique $c$ dans $[a ; b]$ .
| $f$ une fonction définie, continue et strictement croissante sur $[a ; b]$ | $f$ une fonction définie, continue et strictement décroissante sur $[a ; b]$ |
|
|
Remarque
Dans le cas où $f$ est strictement croissante sur $[a ; b]$ , le théorème précédent justifie que :
pour tout $k \in [f(a) ; f(b)]$ , l'équation $f(x) = k$ a une unique solution dans $[a ; b]$ .
On dit que $f$ réalise une bijection de $[a ; b]$ sur $[f(a) ; f(b)]$.
La fonction qui, à tout réel $k$ de $[f(a) ; f(b)]$ associe l'unique réel $c$ de $[a ; b]$ tel que $f(c) = k$ est appelée fonction réciproque de $ f $, elle est notée $f ^{-1}$ .
$f(c) = k$ se traduit alors par $c = f^{ -1} (k) $
Lorsque $f$ est strictement décroissante sur $[a ; b]$ , elle réalise une bijection de $[a ; b]$ sur $[f(b) ; f(a)]$ et on notera de même $f ^{-1}$ sa fonction réciproque.
- Vues: 24185
