Continuité
Exemple 2
· Considérons la fonction $x \mapsto E( x )$ appelée fonction "Partie entière" et qui, à tout réel $x$ associe le plus grand entier inférieur ou égal à $x$ .
Ainsi $E(2,5)$ est le plus grand entier inférieur ou égal à 2,5 , donc $E(2,5) = 2 $
De même $E( - 2,4) = - 2 ; E(1,9999) = 1$ et $ E(2) = 2$
Si $n$ est un nombre entier, alors $ E( n ) = n $
et pour tout $x \in [n ; n + 1 [$ , on a $E( x ) = n$
La représentation graphique de la fonction "Partie entière" est donnée ci-dessous.
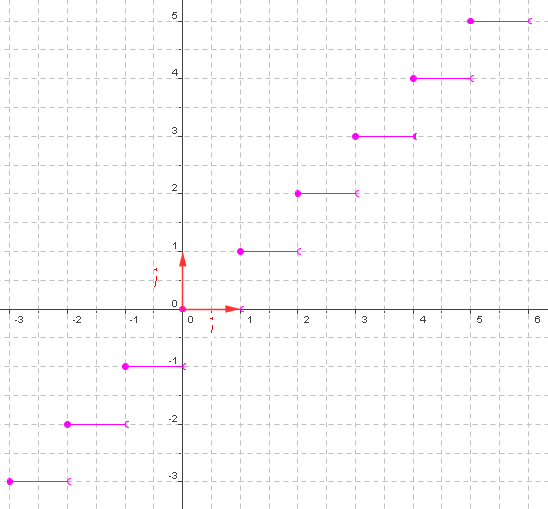
Cette fonction n'est pas continue en $n$ avec $n \in \mathbb{Z} $
En effet lorsque $x$ est très proche de $n$ par valeurs inférieures, $E( x )$ n'est pas très proche de $ E( n )$.
On a vu par exemple que $E(1,9999) = 1$ et $E(2) = 2 $
"Partie entière" est une fonction dite "en escalier".
La courbe fait "un saut" pour chaque valeur de $x$ entière.
Avec une calculatrice TI89, $E( x)$ est noté int( x) ou $floor( x)$, en français $partEnt( x )$
Avec une calculatrice TI82, $E( x )$ est noté int x
Le tracé doit être fait en mode point (dot), \sinon apparaîtront des lignes verticales qui ne font pas partie de la représentation graphique.
Avec un tableur la fonction "Partie entière" est notée ent() .
La somme, le produit, le quotient, la composée de fonctions continues est une fonction continue sur tout intervalle sur lequel elle est définie.
Remarques
La démonstration de cette propriété se fait en utilisant les propriétés des limites.
La plupart des fonctions qui seront étudiées seront des fonctions continues.
- Vues: 23705
