Baccalauréat S Métropole - La Réunion 12 septembre 2017 - Exercice 2
Page 3 sur 10
Exercice 2 5 points
Le plan complexe est rapporté à un repère orthonormé $\left(\text{O},~\vec{u},~\vec{v}\right)$. À tout point $M$ d'affixe $z$, on associe le point $M’$ d'affixe \[z’ = - z^2 + 2z.\] Le point $M’$ est appelé image du point $M$.
- Résoudre dans l'ensemble $ \mathbb{C}$ des nombres complexes l'équation : \[- z^2 + 2z - 2 = 0.\] En déduire les affixes des points dont l'image est le point d'affixe 2.
- Soit $M$ un point d'affixe $z$ et $M’$ son image d'affixe $z’$. On note $N$ le point d'affixe $z_N = z^2$. Montrer que $M$ est le milieu du segment $[NM’]$.
- Dans cette question, on suppose que le point $M$ ayant pour affixe $z$, appartient au cercle $\mathcal{C}$ de centre O et de rayon 1. On note $\theta$ un argument de $z$.
- Déterminer le module de chacun des nombres complexes $z$ et $z_N$, ainsi qu'un argument de $z_N$ en fonction de $\theta$.
- Sur la figure donnée en fin d'exercice, on a représenté un point $M$ sur le cercle $\mathcal{C}$. Construire sur cette figure les points $N$ et $M'$ en utilisant une règle et un compas (on laissera les traits de construction apparents).
- Soit A le point d'affixe 1. Quelle est la nature du triangle A$MM’$ ?
La page contenant l'annexe est à rendre avec la copie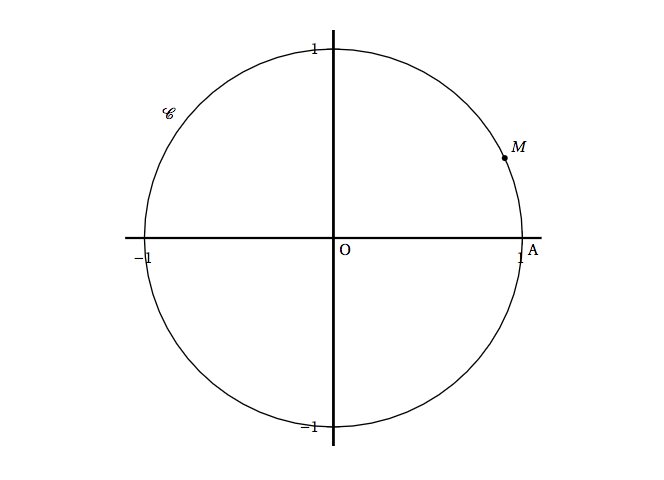
- Vues: 45373
