Baccalauréat S Métropole - La Réunion 12 septembre 2017 - Correction Exercice 4

Page 8 sur 10: Correction Exercice 4

Correction de l'exercice 4 5 points

Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques

Dans l'espace, on considère le cube ABCDEFGH représenté ci-dessous. On note I et J les milieux respectifs des segments [EH] et [FB]. On munit l'espace du repère orthonormé $\left(\text{A}~;~ \vec{\text{AB}},~ \vec{\text{AD}}, \vec{\text{AE}}\right)$.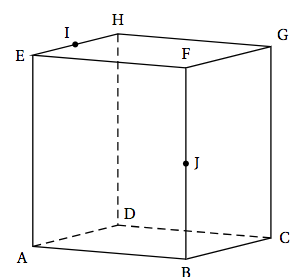

1. Donner les coordonnées des points I et J.
On a $A(0;0;0)$, $B(1;0;0)$, $D(0;1;0)$, $E(0;0;1)$, $H(0;1;1)$ et $F(1;0;1)$.
$I$ est le milieu du segment $[EH]$ donc $I\left(\dfrac{0+0}{2};\dfrac{0+1}{2};\dfrac{1+1}{2}\right)$ soit $I(0;0,5;1)$.
$J$ est le milieu du segment $[FN]$ donc $J\left(\dfrac{1+1}{2};\dfrac{0+0}{2};\dfrac{0+1}{2}\right)$ soit $J(1;0;0,5)$.

2. 1. Montrer que le vecteur $\vec{n}\begin{pmatrix}\phantom{-}1\\- 2\\\phantom{-}2\end{pmatrix}$ est un vecteur normal au plan (BGI).
   On a $\vec{BG}\begin{pmatrix}0\\1\\1\end{pmatrix}$ et $\vec{BI}\begin{pmatrix}-1\\0,5\\1\end{pmatrix}$.
   Ces deux vecteurs ne sont clairement pas colinéaires.
   Par conséquent :
   $\vec{n}.\vec{BG}=0-2+2=0$ et $\vec{n}.\vec{BI}=-1-1+2=0$
   Le vecteur $\vec{n}$ est orthogonal à deux vecteurs non colinéaires du plan $(BGI)$.
   C’est donc un vecteur normal au plan $(BGI)$.
   $\quad$
   
   2. En déduire une équation cartésienne du plan (BGI).
   Une équation cartésienne du plan $(BGI)$ est alors de la forme :
   $$x-2y+2z+d=0$$
   Le point $B(1;0;0)$ appartient à ce plan.
   Donc $1-0+0+d=0 \iff d=-1$.
   Une équation cartésienne du plan $(BGI)$ est donc $x-2y+2z-1=0$.
   $\quad$
   
   3. On note K le milieu du segment [Hl]. Le point K appartient-il au plan (BGI) ?
$K$ est le milieu du segment $[HJ]$.
Donc $K\left(\dfrac{0+1}{2};\dfrac{1+0}{2};\dfrac{1+0,5}{2}\right)$ soit $K(0,5;0,5;0,75)$.
Regardons si les coordonnées de ce point vérifie l’équation du plan $(BGI)$ trouvée à la question précédente.
$0,5-2\times 0,5+2\times 0,75-1=0,5-1+1,5-1=0$.
Donc $K$ appartient au plan $(BGI)$.
$\quad$
3. Le but de cette question est de calculer l'aire du triangle BGI.
   1. En utilisant par exemple le triangle FIG pour base, démontrer que le volume du tétraèdre FBIG est égal à $\dfrac{1}{6}$.
      On rappelle que le volume $V$ d'un tétraèdre est donné par la formule 
      $V = \dfrac{1}{3} B \times h$ où $B$ désigne l'aire d'une base et $h$ la hauteur correspondante.
   Le triangle $FIG$ est isocèle en $I$. Donc en appelant $I’$ le milieu du segment $[FG]$ l’aire de ce triangle est :
   $\mathscr{A}=\dfrac{II’\times FG}{2}=\dfrac{1\times 1}{2}=0,5$.
   Ainsi le volume du tétraèdre $FBIG$ est $\mathscr{V}=\dfrac{\mathscr{A}\times FB}{3}=\dfrac{0,5\times 1}{3}=\dfrac{1}{6}$.
   $\quad$
   
   2. Déterminer une représentation paramétrique de la droite $\Delta$ passant par F et orthogonale au plan (BGI).
   La droite $\Delta$ passe par le point $F(1;0;1)$ est est dirigée par le vecteur $\vec{n}$.
   Une représentation paramétrique de cette droite est donc :
   $\begin{cases} x=1+t\\y=-2t\\z=1+2t\end{cases} \quad, t\in \mathbb{R}$
   $\quad$
   
   3. La droite $\Delta$ coupe le plan (BGI) en F$'$. Montrer que le point F$'$ a pour coordonnées $\left(\frac{7}{9}~;~\frac{4}{9}~;~\frac{5}{9}\right)$.
   Montrons que le points $F’\left(\dfrac{7}{9};\dfrac{4}{9};\dfrac{5}{9}\right)$ appartient à la fois à la droite $\Delta$ et à au plan $(BGI)$.
   Dans la représentation paramétrique de $\Delta$, si on prend $t=-\dfrac{2}{9}$ (solution de l’équation $-2t=\dfrac{4}{9}$ par exemple)alors on obtient :
   $\begin{cases} x=1-\dfrac{2}{9}=\dfrac{7}{9}\\y=-2\times \left(-\dfrac{2}{9}\right)=\dfrac{4}{9}\\z=1-2\times \dfrac{2}{9}=\dfrac{5}{9}\end{cases}$
   Donc $F’\in \Delta$.
   $\dfrac{7}{9}-2\times \dfrac{4}{9}+2\times \dfrac{5}{9}-1=\dfrac{7}{9}-\dfrac{8}{9}+\dfrac{10}{9}-\dfrac{9}{9}=0$
   Donc $F’\in (BGI)$.
   Le vecteur $\vec{n}$ est un vecteur directeur de la droite $\Delta$ et un vecteur normal au plan $(BGI)$: la droite et plan sont donc sécants.
   Le point $F’$ appartient à chacun d’entre eux. C’est donc leur point d’intersection.
   $\quad$
   
   4. Calculer la longueur FF$'$. En déduire l'aire du triangle BGI.
   $FF’=\sqrt{\left(1-\dfrac{7}{9}\right)^2+\left(0-\dfrac{4}{9}\right)^2+\left(1-\dfrac{5}{9}\right)^2}=\dfrac{2}{3}$.
   Le volume du tétraèdre $FBIG$ est :
   $\mathscr{V}=\dfrac{1}{6}\iff \dfrac{FF’\times \text{aire }_{BGI}}{3}=\dfrac{1}{6}$
   Par conséquent l’aire du triangle $BGI$ est $\mathscr{A}’=\dfrac{\dfrac{1}{6}\times 3}{\dfrac{2}{3}}=\dfrac{3}{4}$.