Baccalauréat S Métropole - La Réunion 12 septembre 2017 - Correction Exercice 2

Page 4 sur 10: Correction Exercice 2

Correction de l'exercice 2 (4 points)

 

Le plan complexe est rapporté à un repère orthonormé $\left(\text{O},~\vec{u},~\vec{v}\right)$. À tout point $M$ d'affixe $z$, on associe le point $M’$ d'affixe \[z’ = - z^2 + 2z.\] Le point $M’$ est appelé image du point $M$.

1. Résoudre dans l'ensemble $ \mathbb{C}$ des nombres complexes l'équation : \[- z^2 + 2z - 2 = 0.\] En déduire les affixes des points dont l'image est le point d'affixe 2.
On considère l’équation $-z^2+2z-2=0$.
Son discriminant est $\Delta = 2^2-4\times (-1) \times (-2) = -4<0$
Cette équation possède donc deux racines complexes:
$z_1=\dfrac{-2-\sqrt{4}\text{i}}{-2}=1+\text{i}$ et $z_2=\overline{z_1}=1-\text{i}$
Les points dont l’image est le point d’affixe $2$ vérifie $z’=2 \iff -z^2+2z-2=0$.
Ce sont donc les points d’affixe $1-\text{i}$ et $1+\text{i}$.
$\quad$
2. Soit $M$ un point d'affixe $z$ et $M’$ son image d'affixe $z’$. On note $N$ le point d'affixe $z_N = z^2$. Montrer que $M$ est le milieu du segment $[NM’]$.
On appelle $P$ le milieu du segment $\left[NM’\right]$.
Son affixe est :
$\begin{align*} z_P&=\dfrac{z_n+z_{M’}}{2} \\
&=\dfrac{z^2-z^2+2z}{2} \\
&=z
\end{align*}$
Par conséquent $M$ est le milieu du segment $\left[NM’\right]$
$\quad$
3. Dans cette question, on suppose que le point $M$ ayant pour affixe $z$, appartient au cercle $\mathcal{C}$ de centre O et de rayon 1. On note $\theta$ un argument de $z$.
   1. Déterminer le module de chacun des nombres complexes $z$ et $z_N$, ainsi qu'un argument de $z_N$ en fonction de $\theta$.
   Le point $M$ appartient au cercle $\mathcal{C}$. Par conséquent $|z|=1$ et arg$(z)=\theta$.
   $z_N=z^2=1^2\times \text{e}^{2\text{i} \theta}=\text{e}^{2\text{i}\theta}$
   Ainsi $\left|z_N\right|=1$ et arg$\left(z_N\right)=2\theta$.
   $\quad$
   
   2. Sur la figure donnée en fin d'exercice, on a représenté un point $M$ sur le cercle $\mathcal{C}$. Construire sur cette figure les points $N$ et $M'$ en utilisant une règle et un compas (on laissera les traits de construction apparents).
   
   3. Soit A le point d'affixe 1. Quelle est la nature du triangle A$MM’$ ?
   
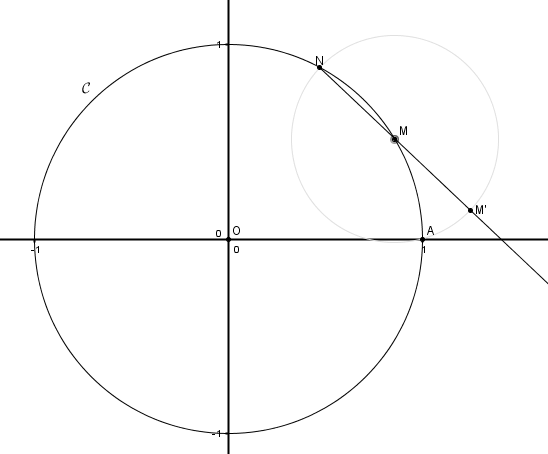
   Le point $N$ appartient au cercle de centre $M$ et de rayon $MA$.
   $M$ est le milieu du segment $\left[NM’\right]$. Ainsi $MN=MM’$.
   Donc $MA=MM’$.
   Le triangle $AMM’$ est par conséquent isocèle en $M$.

Commun à tous les candidats