Baccalauréat S Métropole - La Réunion 12 septembre 2017 - Exercice 4
Page 7 sur 10
Exercice 4 5 points
Dans l'espace, on considère le cube ABCDEFGH représenté ci-dessous. On note I et J les milieux respectifs des segments [EH] et [FB]. On munit l'espace du repère orthonormé $\left(\text{A}~;~ \vec{\text{AB}},~ \vec{\text{AD}}, \vec{\text{AE}}\right)$. 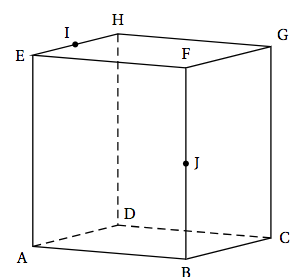
- Donner les coordonnées des points I et J.
-
- Montrer que le vecteur $\vec{n}\begin{pmatrix}\phantom{-}1\\- 2\\\phantom{-}2\end{pmatrix}$ est un vecteur normal au plan (BGI).
- En déduire une équation cartésienne du plan (BGI).
- On note K le milieu du segment [Hl]. Le point K appartient-il au plan (BGI) ?
- Le but de cette question est de calculer l'aire du triangle BGI.
- En utilisant par exemple le triangle FIG pour base, démontrer que le volume du tétraèdre FBIG est égal à $\dfrac{1}{6}$.
On rappelle que le volume $V$ d'un tétraèdre est donné par la formule
$V = \dfrac{1}{3} B \times h$ où $B$ désigne l'aire d'une base et $h$ la hauteur correspondante. - Déterminer une représentation paramétrique de la droite $\Delta$ passant par F et orthogonale au plan (BGI).
- La droite $\Delta$ coupe le plan (BGI) en F$'$. Montrer que le point F$'$ a pour coordonnées $\left(\frac{7}{9}~;~\frac{4}{9}~;~\frac{5}{9}\right)$.
- Calculer la longueur FF$'$. En déduire l'aire du triangle BGI.
- En utilisant par exemple le triangle FIG pour base, démontrer que le volume du tétraèdre FBIG est égal à $\dfrac{1}{6}$.
- Vues: 45376
