Baccalauréat S Pondichéry 22 avril 2016 - Correction Exercice 5
Correction Exercice 5 5 points
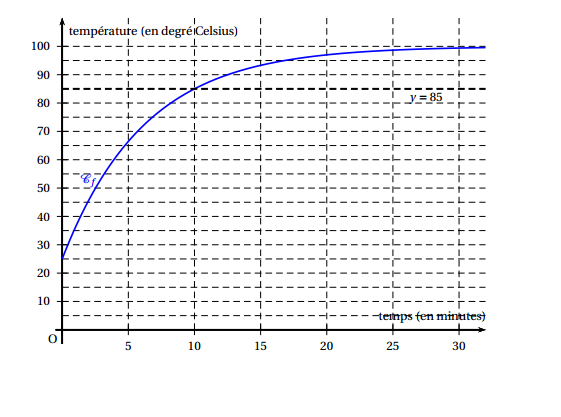
On souhaite stériliser une boîte de conserve. Pour cela, on la prend à la température ambiante $T_0 = 25$degrés C et on la place dans un four à température constante $T_F = 100$degrés C. La stérilisation débute dès lors que la température de la boîte est supérieure à 85degrés C.
Les deux parties de cet exercice sont indépendantes
Partie A : Modélisation discrète
Pour $n$ entier naturel, on note $T_n$ la température en degré Celsius de la boîte au bout de $n$ minutes. On a donc $T_0 = 25$. Pour $n$ non nul, la valeur $T_n$ est calculée puis affichée par l'algorithme suivant : $$\begin{array}{ |l|l|}\hline \text{Initialisation :} & T \text{ prend la valeur 25}\\ \hline \text{ Traitement :} & \text{ Demander la valeur de } n \\ & \text{ Pour } i \text{ allant de } 1 \text{ à } n \text{ faire}\\ &\hspace{0,5cm} T \text{ prend la valeur } 0,85 \times T + 15 \\ & \text{ Fin Pour }\\ \hline \text{ Sortie :} & \text{ Afficher }T\\ \hline \end{array} $$
- Déterminer la température de la boîte de conserve au bout de 3 minutes. Arrondir à l'unité. $T_0=25$, $T_1=36,25$, $T_2=45,8125$ et $T_3=53,940625$.
- Démontrer que, pour tout entier naturel $n$, on a $T_n = 100 - 75 \times 0,85^n$. Montrons par récurrence que, pour tout entier naturel $n$ on a $T_n=100-75\times 0,85^n$.
- Au bout de combien de minutes la stérilisation débute-elle ? La stérilisation débute quand $T_n>85$.
Ainsi la température de la boîte arrondie à l’unité est de $54$°C.
$\quad$
Initialisation : Si $n=0$, $T_0=25$ et $100-75\times 0,85^0=100-75=25$.
La propriété est donc vraie au rang $0$.
$\quad$
Hérédité : Supposons la propriété vraie au rang $n$ : $T_n=100-75\times 0,85^n$.
$\begin{align*} T_{n+1}&=0,85 \times T_n+15 \\
&=0,85 \times \left(100-75\times 0,85^n\right)+15 \\
&=85-75\times 0,85^{n+1}+15 \\
&=100-75\times 0,85^{n+1}
\end{align*}$
La propriété est donc vraie au rang $n+1$.
$\quad$
Conclusion : La propriété est donc vraie au rang $0$ et est héréditaire.
Par conséquent, pour tout entier naturel $n$, $T_n=100-75\times 0,85^n$.
$\quad$
On résout donc :
$\begin{align*} 100-75\times 0,85^n > 85 &\Leftrightarrow -75\times 0,85^n > -15 \\
&\Leftrightarrow 0,85^n < 0,2 \\
&\Leftrightarrow n\ln 0,85 < \ln 0,2 \\
&\Leftrightarrow n> \dfrac{\ln 0,2}{\ln 0,85}
&\Leftrightarrow n \geqslant 10
\end{align*}$
La stérilisation commence donc au bout de $10$ minutes.
$\quad$
Partie B : Modélisation continue
Dans cette partie, $t$ désigne un réel positif. On suppose désormais qu'à l'instant $t$ (exprimé en minutes), la température de la boîte est donnée par $f(t)$ (exprimée en degré Celsius) avec : \[f(t) = 100 - 75\text{e}^{- \frac{\ln 5}{10}t}.\]
-
- Étudier le sens de variations de $f$ sur $[0~;~+ \infty[$. $f$ est une fonction dérivable sur $[0;+\infty[$ en tant que somme de fonctions dérivables sur cet intervalle.
- Justifier que si $t \geqslant 10$ alors $f(t) \geqslant 85$.
$f'(t)=75\times \dfrac{\ln 5}{10}\text{e}^{-\frac{\ln 5}{10}t} > 0$ car la fonction exponentielle est toujours strictement positive.
Donc $f$ est strictement croissante sur $[0;+\infty[$.
$\quad$
Puisque la fonction $f$ est strictement croissante sur $[0;+\infty[$, alors, pour tout $t\geqslant 10$ alors $f(t) \geqslant f(10)$ soit $f(t)\geqslant 85$.
$\quad$ - Soit $\theta$ un réel supérieur ou égal à 10. On note $\mathcal{A}(\theta)$ le domaine délimité par les droites d'équation $t = 10,\: t = \theta,\:$ $y = 85$ et la courbe représentative $\mathcal{C}_f$ de $f$. On considère que la stérilisation est finie au bout d'un temps $\theta$, si l'aire, exprimée en unité d'aire du domaine $\mathcal{A}(\theta)$ est supérieure à $80$.
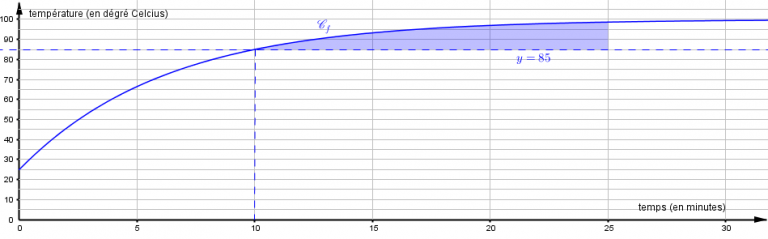
- Justifier, à l'aide du graphique donné en annexe , que l'on a $\mathcal{A}(25) > 80$. Chaque rectangle a une aire de $5\times 5$ unités d’aires.
- Justifier que, pour $\theta \geqslant 10$, on a $\mathcal{A}(\theta) = 15(\theta - 10) - 75 \displaystyle\int_{10}^{\theta} \text{e}^{- \frac{\ln 5}{10}t}\:\text{d}t$. $\begin{align*} A(\theta)&=\displaystyle \int_{10}^{\theta} (f(t)-85)\mathrm{d}t \\
- La stérilisation est-elle finie au bout de 20 minutes ? $\begin{align*} \int_{10}^{\theta}\text{e}^{-\frac{\ln 5}{10}t}\mathrm{d}t &=- \dfrac{10}{\ln 5}\left[\text{e}^{-\frac{\ln 5}{10}t}\right]_{10}^{\theta} \\
$3$ rectangles complets sont inclus dans la partie coloriée et en prenant deux des morceaux de rectangles restants on obtient une aire supérieure à celle d’un quatrième rectangle.
L’aire coloriée est donc supérieure ou égale à $4\times 5\times 5 = 100 > 80$.
Donc $A(25)>80$.
&=\int_{10}^{\theta}\left(15-75\text{e}^{-\frac{\ln 5}{10}t}\right)\mathrm{d}t \\
&=\int_{10}^{\theta}15\mathrm{d}t-\int_{10}^{\theta}75\text{e}^{-\frac{\ln 5}{10}t}\mathrm{d}t \\
&=15(\theta-10)-\int_{10}^{\theta}75\text{e}^{-\frac{\ln 5}\\{10}t}\mathrm{d}t \\
&=15(\theta-10)-75\int_{10}^{\theta}\text{e}^{-\frac{\ln 5}{10}t}\mathrm{d}t
\end{align*}$
&=-\dfrac{10}{\ln 5}\left(\text{e}^{-\frac{\ln 5}{10}\theta}-\dfrac{1}{5}\right)
\end{align*}$
Ainsi $A(20)=150 + 75\times \dfrac{10}{\ln 5}\left(\text{e}^{-\frac{\ln 5}{10}\times 20}-\dfrac{1}{5}\right) \approx 75,4 <80$.
La stérilisation n’est donc pas terminée au bout de $20$ minutes.
- Vues: 35088