Baccalauréat S Pondichéry 22 avril 2016 - Correction Exercice 4
Correction de l'exercice 4 3 points
Soit $f$ la fonction définie sur $]0~;~14]$ par \[f(x) = 2 - \ln\left(\dfrac{x}{2}\right).\] La courbe représentative $\mathcal{C}_f$ de la fonction $f$ est donnée dans le repère orthogonal d'origine O ci-dessous :
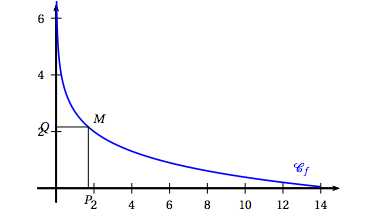
À tout point $M$ appartenant à $\mathcal{C}_f$ on associe le point $P$ projeté orthogonal de $M$ sur l'axe des abscisses, et le point $Q$ projeté orthogonal de $M$ sur l'axe des ordonnées.
- L'aire du rectangle O$PMQ$ est-elle constante quelle que soit la position du point $M$ sur $\mathcal{C}_f$ ?
- L'aire du rectangle O$PMQ$ peut-elle être maximale ? Si oui, préciser les coordonnées du point $M$ correspondant.
Justifier les réponses.
On a $O(0;0)$, $P(x;0)$, $M(x;f(x))$ et $Q(0;f(x))$.
Donc l’aire du rectangle $OPMQ$ est $\mathscr{A}(x)=xf(x)=2x-x\ln \left(\dfrac{x}{2}\right)$.
Cette fonction $\mathscr{A}$ définie sur $]0;14]$ est dérivable sur cet intervalle en tant que somme et produits de fonctions dérivables sur cet intervalle.
$\mathscr{A}'(x)=2-\ln \left(\dfrac{x}{2}\right)-x\times \dfrac{1}{2}\times \dfrac{1}{\dfrac{x}{2}}=1-\ln \left(\dfrac{x}{2}\right)$.
Or :
$\begin{align*} 1-\ln \left(\dfrac{x}{2}\right) = 0 &\Leftrightarrow \ln \left(\dfrac{x}{2}\right) = 1 \\
&\Leftrightarrow \dfrac{x}{2}=\text{e}\\
&\Leftrightarrow x=2\text{e}
\end{align*}$
De même :
$\begin{align*} 1-\ln \left(\dfrac{x}{2}\right) > 0 &\Leftrightarrow \ln \left(\dfrac{x}{2}\right) < 1 \\
&\Leftrightarrow \dfrac{x}{2}<\text{e} \\
&\Leftrightarrow x<2\text{e}
\end{align*}$
Ainsi la fonction $\mathscr{A}$ admet un maximum pour $x=2\text{e}$.
$f\left(2\text{e}\right)=2-\ln\left(\dfrac{2e}{2}\right)=2-\ln \text{e} = 1$.
Par conséquent l’aire du rectangle $OPMQ$ n’est pas constante. Elle peut être maximale. Cela se produit pour $M(2\text{e};1)$
$\quad$
- Vues: 35015
