Baccalauréat S Pondichéry 22 avril 2016 - Exercice 2
Page 3 sur 13
Exercice 2 3 points
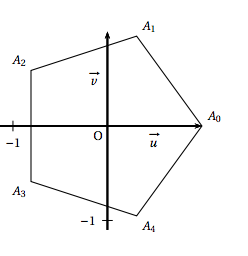
Dans le plan complexe muni d'un repère orthonormé direct $(O; \vec {u}, \vec{v})$, on considère le pentagone régulier $A_0A_1A_2A_3A_4$, de centre $O$ tel que $\vec{OA_0} = \vec{u}$. On rappelle que dans le pentagone régulier $A_0A_1A_2A_3A_4$, ci-contre :
- les cinq côtés sont de même longueur;
- les points $A_0,\:A_1,\:A_2,\:A_3$ et $A_4$ appartiennent au cercle trigonométrique ;
- pour tout entier $k$ appartenant à $\{0~;~1~;~2~;~3\}$ on a $\left(\vec{OA_k}~;~\vec{OA_{k+1}}\right) = \dfrac{2\pi}{5}$.
- On considère les points $B$ d'affixe $- 1$ et $J$ d'affixe $\dfrac{\text{i}}{2}$. Le cercle $(\mathcal{C})$ de centre $J$ et de rayon $\dfrac{1}{2}$ coupe le segment $[BJ]$ en un point $K$. Calculer $BJ$, puis en déduire $BK$.
- Donner sous forme exponentielle l'affixe du point $A_2$. Justifier brièvement.
- Démontrer que $BA_2\,^2 = 2 + 2\cos \left(\dfrac{4\pi}{5}\right)$.
- Un logiciel de calcul formel affiche les résultats ci-dessous, que l'on pourra utiliser sans justification : $$\begin{array}{|c|c|}\hline \blacktriangleright \text{ Calcul formel}\\\hline 1&cos (4*pi/5)\\ & \to \dfrac{1}{4}\left(- \sqrt{5} - 1\right) \\ \hline 2& sqrt((3 - sqrt(5))/2)\\ \hline & \to \dfrac{1}{2}\left(\sqrt{5} - 1\right) \\ \hline \end{array}$$ « sqrt » signifie « racine carrée» En déduire, grâce à ces résultats, que $BA_2 = BK$.
- Dans le repère $(O; \vec {u}, \vec{v})$ donné en annexe, construire à la règle et au compas un pentagone régulier.
N'utiliser ni le rapporteur ni les graduations de la règle et laisser apparents les traits de construction.
- Vues: 40027
