Baccalauréat S Pondichéry 22 avril 2016 - Exercice 3
Page 5 sur 13
Exercice 3 5 points
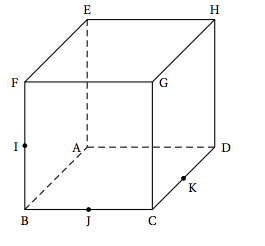
ABCDEFGH désigne un cube de côté 1. Le point I est le milieu du segment [BF]. Le point J est le milieu du segment [BC]. Le point K est le milieu du segment [CD].}
Partie A
Dans cette partie, on ne demande aucune justification
On admet que les droites (IJ) et (CG) sont sécantes en un point L. Construire, sur la figure fournie en annexe et en laissant apparents les traits de construction:
- le point L ;
- l'intersection $\mathcal{D}$ des plans (IJK) et (CDH) ;
- la section du cube par le plan (IJK).
Partie B
L'espace est rapporté au repère $\left(\text{A}~;~\vec{\text{AB}},~\vec{\text{AD}},~\vec{\text{AE}}\right)$.
- Donner les coordonnées de A, G, I, J et K dans ce repère.
-
- Montrer que le vecteur $\vec{\text{AG}}$ est normal au plan (IJK).
- En déduire une équation cartésienne du plan (IJK).
- On désigne par $M$ un point du segment [AG] et $t$ le réel de l'intervalle [0~;~1] tel que $\vec{\text{A}M} = t\vec{\text{AG}}$.
- Démontrer que $M\text{I}^2 = 3t^2 - 3t + \dfrac{5}{4}$.
- Démontrer que la distance $M$I est minimale pour le point $M\left(\dfrac{1}{2}~;~\dfrac{1}{2}~;~\dfrac{1}{2}\right)$.
- Démontrer que pour ce point $M\left(\dfrac{1}{2}~;~\dfrac{1}{2}~;~\dfrac{1}{2}\right)$ :
- $M$ appartient au plan (IJK).
- La droite (I$M$) est perpendiculaire aux droites (AG) et (BF).
- Vues: 34767
