Baccalauréat S Amérique du Nord 1er juin 2016 - Correction Exercice 4

Page 8 sur 10: Correction Exercice 4

Correction de l'exercice 4 5 points

Candidats N'AYANT PAS SUIVI l'enseignement de spécialité mathématiques

On considère la pyramide régulière SABCD de sommet S constituée de la base carrée ABCD et de triangles équilatéraux représentée ci-dessous.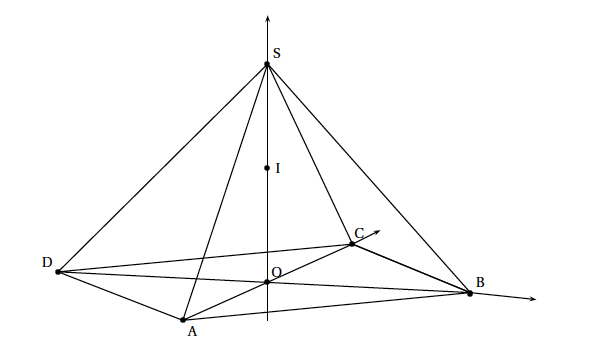

Le point O est le centre de la base ABCD avec OB $= 1$. On rappelle que le segment [SO] est la hauteur de la pyramide et que toutes les arêtes ont la même longueur.

1. Justifier que le repère $\left(\text{O}~;~ \vec{\text{OB}},~\vec{\text{OC}},~\vec{\text{OS}}\right)$ est orthonormé. Dans la suite de l'exercice, on se place dans le repère $\left(\text{O}~;~ \vec{\text{OB}},~\vec{\text{OC}},~\vec{\text{OS}}\right)$.
$ABCD$ est un carré de centre $O$ tel que $OB=1$.
Ainsi $OB=OC=1$.
Les diagonales d’un carré sont perpendiculaires donc $\vec{OB}.\vec{OC}=0$.
$[OS]$ est la hauteur de la pyramide donc $(OS)$ est perpendiculaire au plan $(OBC)$. Ainsi $\vec{OS}$ est orthogonal à $\vec{OB}$ et $\vec{OC}$.
Il ne reste plus qu’à montrer que $OS=1$.
Dans le triangle $OBC$ rectangle en $O$ on applique le théorème de Pythagore.
Ainsi $BC^2=OB^2+OC^2=2$ donc $BC=\sqrt{2}$.
Toutes les arrêtes ayant la même longueur, on a également $AS=\sqrt{2}$.
Dans le triangle $OAS$ rectangle en $O$ on applique le théorème de Pythagore :
$\begin{align*} AS^2=OS^2+OA^2&\iff 2=OS^2+1 \\
&\iff 1=OS^2 \\
&\iff OS=1
\end{align*}$
Le repère $\left(O;\vec{OB},\vec{OC},\vec{OS}\right)$ est donc orthonormé.
$\quad$
2. On définit le point K par la relation $\vec{\text{SK}} = \dfrac{1}{3} \vec{\text{SD}}$ et on note I le milieu du segment [SO].
   1. Déterminer les coordonnées du point K.
   $\vec{OD}=-\vec{OB}$. Donc les coordonnées de $D$ sont $(-1;0;0)$. On a de plus $S(0;0;1)$
   Ainsi $\vec{SD}(-1;0;-1)$.
   Par conséquent :
   $\begin{align*} \vec{SK}=\dfrac{1}{3}\vec{SD} &\iff \begin{cases} x_K = \dfrac{1}{3}\times (-1) \\y_K=\dfrac{1}{3}\times 0 \\z_K-1=\dfrac{1}{3}\times (-1) \end{cases} \\
   &\iff \begin{cases} x_k=-\dfrac{1}{3} \\y_k=0 \\z_k=1-\dfrac{1}{3} \end{cases} \\
   &\iff K\left(-\dfrac{1}{3};0;\dfrac{2}{3}\right)
   \end{align*}$
   $\quad$
   
   2. En déduire que les points B, I et K sont alignés.
   $I(0;0;0,5)$ et $B(1;0;0)$
   Ainsi $\vec{BI}(-1;0;0,5)$
   $\vec{BK}\left(-\dfrac{4}{3};0;\dfrac{2}{3}\right)$
   Ainsi $\vec{BK}=\dfrac{4}{3}\vec{BI}$.
   Les vecteurs sont donc colinéaires et les points $B$, $I$ et $K$ sont alignés.
   $\quad$
   
   3. On note L le point d'intersection de l'arête [SA] avec le plan (BCI). Justifier que les droites (AD) et (KL) sont parallèles.
   On appelle $L’$ le point défini par la relation $\vec{SL’}=\dfrac{1}{3}\vec{SA}$.
   Pour les mêmes raisons qu’à la question précédente $C$, $I$ et $L’$ sont alignés.
   Ainsi $L’$ est l’intersection de $(CI)$ et de $(SA)$.
   Donc $L=L’$.
   Par conséquent :
   $\begin{align*} \vec{LK}&=\vec{LS}+\vec{SK} \\
   &=\dfrac{1}{3}\vec{AS}+\dfrac{1}{3}\vec{SD} \\
   &=\dfrac{1}{3}\left(\vec{AS}+\vec{SD}\right) \\
   &=\dfrac{1}{3}\vec{AD}
   \end{align*}$
   Les droites $(AD)$ et $(KL)$ sont donc parallèles.
   $\quad$
   
   4. Déterminer les coordonnées du point L.
   $A(0;-1;0)$ et $D(-1;0;0)$ donc $\vec{AD}(-1;1;0)$.
   Par conséquent :
   $\begin{align*} \vec{LK}=\dfrac{1}{3}\vec{AD} &\iff \begin{cases} -\dfrac{1}{3}-x_L = \dfrac{-1}{3} \\0-y_L=\dfrac{1}{3} \\ \dfrac{2}{3}-z_L=0 \end{cases} \\
   &\iff \begin{cases} x_L=0 \\ y_L=-\dfrac{1}{3}\\z_L=\dfrac{2}{3}\end{cases} \end{align*}$
   $\quad$
3. On considère le vecteur $\vec{n}\begin{pmatrix}1\\1\\2\end{pmatrix}$ dans le repère $\left(\text{O}~;~ \vec{\text{OB}},~\vec{\text{OC}},~\vec{\text{OS}}\right)$.
   1. Montrer que $\vec{n}$ est un vecteur normal au plan (BCI).
   $\vec{BC}(-1;1;0)$ donc $\vec{BC}.\vec{n}=-1+1+0=0$.
   $\vec{BI}(-1;0;0,5)$ donc $\vec{BI}.\vec{n}=-1+0+1=0$.
   Les deux vecteurs $\vec{BI}$ et $\vec{BC}$ ne sont clairement pas colinéaires.
   Le vecteurs $\vec{n}$ est donc orthogonal à deux vecteurs non colinéaires du plan $(BCI)$. Il est par conséquent normal à ce plan.
   $\quad$
   
   2. Montrer que les vecteurs $\vec{n},\: \vec{\text{AS}}$ et $\vec{\text{DS}}$ sont coplanaires.
   On a $\vec{AS} \begin{pmatrix}0\\1\\1\end{pmatrix}$ et $\vec{DS} \begin{pmatrix}1\\0\\1\end{pmatrix}$
   Donc $\vec{n}=\vec{AS}+\vec{DS}$.
   Ces trois vecteurs sont par conséquent coplanaires.
   $\quad$
   
   3. Quelle est la position relative des plans (BCI) et (SAD) ?
   Il existe donc une droite de $(SAD)$ dont un vecteur directeur est $\vec{n}$.
   Cette droite est par conséquent perpendiculaire au plan $(BCI)$.
   Les plans $(SAD)$ et $(BCI)$ sont donc perpendiculaires.