Baccalauréat S Amérique du Sud 22 novembre 2016
Page 1 sur 12
Exercice 1 5 points
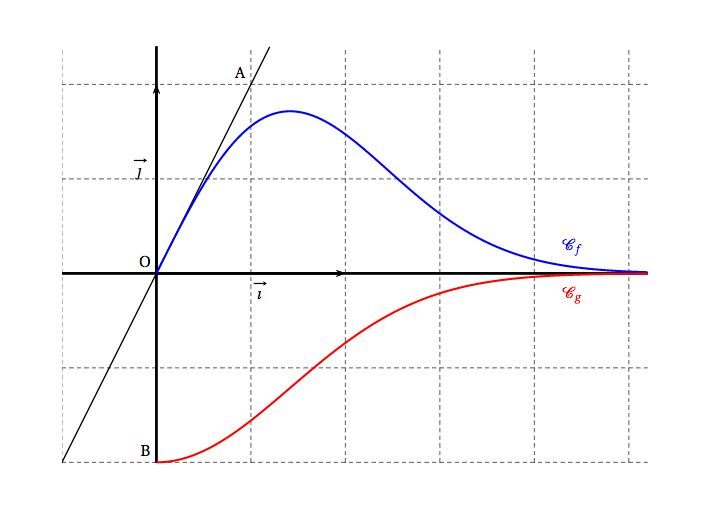
Les courbes $\mathcal{C}_f$ et $\mathcal{C}_g$ données en annexe 1 sont les représentations graphiques, dans un repère orthonormé $\left(\text{O},~\vec{\imath},~\vec{\jmath}\right)$, de deux fonctions $f$ et $g$ définies sur $[0~;~+ \infty[$. On considère les points A(0,5 ; 1) et B$(0 ; -1)$ dans le repère $\left(\text{O},~\vec{\imath},~\vec{\jmath}\right)$. On sait que O appartient à $\mathcal{C}_f$ et que la droite (OA) est tangente à $\mathcal{C}_f$ au point O.
- On suppose que la fonction $f$ s'écrit sous la forme $f(x) = (ax + b)\text{e}^{- x^2}$ où $a$ et $b$ sont des réels. Déterminer les valeurs exactes des réels $a$ et $b$, en détaillant la démarche.
-
- On admettra que, pour tout réel $x$ strictement positif, $f(x) = \dfrac{2}{x}\times \dfrac{x^2}{\text{e}^{x^2}}$. Calculer $\displaystyle\lim_{x \to + \infty} f(x)$.
- Dresser, en le justifiant, le tableau de variations de la fonction $f$ sur $[0~;~+ \infty[$.
- La fonction $g$ dont la courbe représentative $\mathcal{C}_g$ passe par le point B$(0~;~-1)$ est une primitive de la fonction $f$ sur $[0~;~+ \infty[$.
- Déterminer l'expression de $g(x)$.
- Soit $m$ un réel strictement positif. Calculer $I_m = \displaystyle\int_0^{m} f(t)\:\text{d}t$ en fonction de $m$.
- Déterminer $\displaystyle\lim_{m \to + \infty} I_m$.
-
- Justifier que $f$ est une fonction densité de probabilité sur $[0~;~+ \infty[$.
- Soit $X$ une variable aléatoire continue qui admet la fonction $f$ comme densité de probabilité. Justifier que, pour tout réel $x$ de $[0~;~+ \infty[$, $P(X \leqslant x) = g(x) + 1$.
- En déduire la valeur exacte du réel $\alpha$ tel que $P(X \leqslant \alpha) = 0,5$.
- Sans utiliser une valeur approchée de $\alpha$, construire dans le repère de l'annexe 1 le point de coordonnées $(\alpha~;~0)$ en laissant apparents les traits de construction. Hachurer ensuite la région du plan correspondant à $P(X \leqslant \alpha)$.
Désormais, on considère que $f(x) = 2x\text{e}^{- x^2}$ pour tout $x$ appartenant à $[0~;~+ \infty[$
Annexe de l'exercice 1
- Vues: 47733
