Baccalauréat S Centres étrangers 10 juin 2015 - Correction Exercice 1
Correction de l'exercice 1 (5 points)
Tous les résultats demandés dans cet exercice seront arrondis au millième.
Les parties A, B et C sont indépendantes.
Un fournisseur produit deux sortes de cadenas. Les uns sont premier prix, et les autres sont haut de gamme. Un magasin de bricolage dispose d'un stock de cadenas provenant de ce fournisseur; ce stock comprend un grand nombre de cadenas de chaque type.
Partie A
- Le fournisseur affirme que, parmi les cadenas haut de gamme, il n'y a pas plus de 3% de cadenas défectueux dans sa production. Le responsable du magasin de bricolage désire vérifier la validité de cette affirmation dans son stock ; à cet effet, il prélève un échantillon aléatoire de 500 cadenas haut de gamme, et en trouve 19 qui sont défectueux.
Ce contrôle remet-il en cause le fait que le stock ne comprenne pas plus de 3% de cadenas défectueux ? On pourra pour cela utiliser un intervalle de fluctuation asymptotique au seuil de 95%. - Le responsable du magasin souhaite estimer la proportion de cadenas défectueux dans son stock de cadenas premier prix. Pour cela il prélève un échantillon aléatoire de 500 cadenas premier prix , parmi lesquels 39 se révèlent défectueux.
Donner un intervalle de confiance de cette proportion au niveau de confiance 95%. - On arrondit la borne inférieure par défaut à $10^{-\7}$ près : $\1 - \dfrac{1}{\sqrt{\2}}\approx \10$ soit $\5$.
- On arrondit la borne supérieure par excés à $10^{-\7}$ près : $\1 + \dfrac{1}{\sqrt{\2}}\approx \11$ soit $\6$.
La proportion $p$ est égale à $\1$. La taille $n$ de l'échantillon considéré est égale à $\2.$
Comme $ n =\2$ , $n \times p $=\3 et $n\times (1-p)=\4,$ les conditions d'utilisation d'un intervalle de fluctuation asymptotique sont réunies.
L'intervalle de fluctuation asymptotique au seuil de $95\% $ est : $$I_{\2} = \left[\1 - 1,96\sqrt{\dfrac{\1\times \5}{\2}}~;~\1 + 1,96\sqrt{\dfrac{\1\times \5}{\2}} \right]$$
La fréquence observée est $f = \dfrac{19}{500} = 0,038 \in I_{500}$.
Ce contrôle ne remet donc pas en cause, au risque de $5\%$, l’affirmation du fournisseur.
$\quad$
La fréquence est égale à $\1$. La taille $n$ de l'échantillon considéré est égale à $\2.$
Comme $ n =\2$ , $n \times \8 =\3$ et $n\times (1-\8)=\4,$ les conditions d'utilisation d'un intervalle de confiance sont réunies.
L' intervalle de confiance avec un niveau de confiance de 95% est : \[I = \left[f - \dfrac{1}{\sqrt{n}}~;~f +\dfrac{1}{\sqrt{n}} \right]\]
La fréquence est $\8=\1$.
L'intervalle de confiance au niveau de 95% est \[\9 = \left[\1 - \dfrac{1}{\sqrt{\2}}~;~\1 + \dfrac{1}{\sqrt{\2}} \right]\approx[\5~;~\6]\]
Partie B
D'après une étude statistique faite sur plusieurs mois, on admet que le nombre X de cadenas premier prix vendus par mois dans le magasin de bricolage peut être modélisé par une variable aléatoire qui suit la loi normale de moyenne $\mu = 750$ et d'écart-type $\sigma = 25$.
- Calculer $P(725 \leqslant X \leqslant 775)$.
- Le responsable du magasin veut connaître le nombre $n$ de cadenas premier prix qu'il doit avoir en stock en début de mois, pour que la probabilité d'être en rupture de stock en cours de mois soit inférieure à 0,05. On ne réalimente pas le stock en cours de mois .
Déterminer la plus petite valeur de l'entier $n$ remplissant cette condition. On cherche donc la valeur de $n$ telle que $P(X>n) = 0,05$
2ND DISTR 2NORMALFRép( \1 , \2,\3,\4)EXE
Avec une calculatrice de type TI
$$NormalFR\text{é}p(\1,\2,\3,\4) \approx \5$$
Remarque : Une propriété du cours nous la donne aussi :
Si $X$ suit $\mathcal{N}(\mu; \sigma)$, alors : $$P(\mu- \sigma \leqslant X \leqslant \mu+ \sigma)\approx 0,683$$
Ou encore $P(X \le n) = 0,95$.
A l’aide de la touche « invnorm » ou « normalFRép » de la calculatrice, on trouve $n= 792$ (on arrondit par excès).
2ND DISTR 2Fracnormale( \1 , \2, \3 )EXE
Avec une calculatrice de type TI $FracNormale(\1,\2,\3) \approx \4$
$\quad$
Une autre méthode consiste à se ramener à la loi normale centrée réduite:
En effet $Z=\dfrac{X-\mu}{\sigma}=\dfrac{X-750}{25} $ suit $\mathcal{N}(0;1)$ $$\begin{array}{rl} P(X \le n) = 0,95 & \iff P\left(\dfrac{X-750}{25} \le \dfrac{n-750}{25}\right) = 0,95 \\ &\iff P\left(Z \le \dfrac{n-750}{25}\right) = 0,95 \\ &\iff \pi\left(\dfrac{n-750}{25}\right)=0,95\\ &\iff \dfrac{n-750}{25} = \pi^{-1}(0,95) \\ &\iff n-750 = 25\pi^{-1}(0,95) \\ &\iff n = 750 + 25\pi^{-1}(0,95) \\ &\iff n = 750 + 25FracNormale(0,95) \\ &\iff n \approx 791,1 \\ \end{array}$$
Partie C
On admet maintenant que, dans le magasin :
- 80% des cadenas proposés à la vente sont premier prix, les autres haut de gamme ;
- 3% des cadenas haut de gamme sont défectueux ;
- 7% des cadenas sont défectueux.
On prélève au hasard un cadenas dans le magasin. On note :
- $p$ la probabilité qu'un cadenas premier prix soit défectueux ;
- $H$ l'évènement : « le cadenas prélevé est haut de gamme » ;
- $D$ l'évènement : « le cadenas prélevé est défectueux ».
- Représenter la situation à l'aide d'un arbre pondéré.
- Exprimer en fonction de $p$ la probabilité $P(D)$. En déduire la valeur du réel $p$. Le résultat obtenu est-il cohérent avec celui de la question A - 2. ? D’après la formule des probabilités totales on a :
- Le cadenas prélevé est en bon état. Déterminer la probabilité que ce soit un cadenas haut de gamme . On veut calculer :
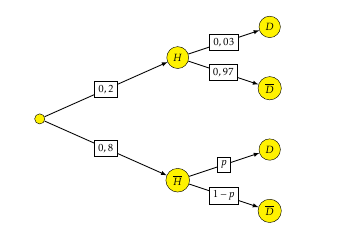
$$\begin{array}{rl} p(D) &= p(H \cap D) + p\left(\overline{H} \cap D\right) \\ 0,07&= 0,2 \times 0,03 + 0,8p \\ 0,07 & = 0,006 + 0,8p \\ 0,064 &= 0,8p \\ p&= \dfrac{0,064}{0,8}\\ p&= 0,08
\end{array}$$
$\quad$ $0,08 \in [0,033;0,123]$.
Ce résultat est donc cohérent avec celui de la question A-2.
$\quad$
$$\begin{array}{rl} P_{\overline{D}}(H) &= \dfrac{p\left(\overline{D}\cap H\right)}{p\left(\overline{D}\right)} \\ &=\dfrac{0,2 \times 0,97}{1 – 0,07} \\ & \approx 0,209
\end{array}$$
- Vues: 47218
