Baccalauréat S Centres étrangers 10 juin 2015 - Exercice 4
Exercice 4 5 points
Les parties A et B sont indépendantes
Le fabricant de cadenas de la marque « K » désire imprimer un logo pour son entreprise.
Ce logo a la forme d'une lettre majuscule K stylisée, inscrite dans un carré ABCD, de côté une unité de longueur, et respectant les conditions C1 et C2 suivantes:
$\bullet~~$Condition C1 : la lettre K doit être constituée de trois lignes :
- une des lignes est le segment [AD] ;
- une deuxième ligne a pour extrémités le point A et un point E du segment [DC] ;
- la troisième ligne a pour extrémité le point B et un point G situé sur la deuxième ligne.
$\bullet~~$Condition C2 : l'aire de chacune des trois surfaces délimitées par les trois lignes dessinées dans h le carré doit être comprise entre $0,3$ et $0,4$, l'unité d'aire étant celle du carré. Ces aires sont notées $r$, $s$, $t$ sur les figures ci-après.
Un atelier de design propose deux dessins possibles, représentés ci-dessous: 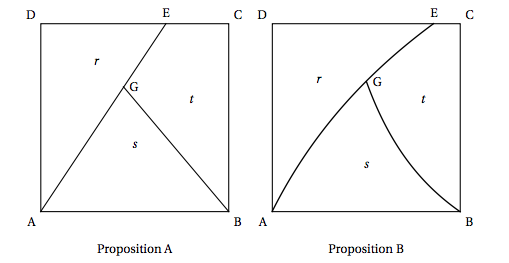
Pour mener les études qui suivent, on se place dans le repère orthonormé $\left(\text{A}~;~\vec{\text{AB}},~\vec{\text{AD}}\right)$.
Partie A : étude de la proposition A
Dans cette proposition les trois lignes sont des segments et les trois aires sont égales : $r = s = t = \dfrac{1}{3}$.
Déterminer les coordonnées des points E et G.
Partie B : étude de la proposition B
Cette proposition est caractérisée par les deux modalités suivantes:
$\bullet~~$la ligne d'extrémités A et E est une portion de la représentation graphique de la fonction $f$ définie pour tout réel $x \geqslant 0$ par : $f(x) = \ln (2x + 1)$ ;
$\bullet~~$la ligne d'extrémités B et G est une portion de la représentation graphique de la fonction $g$ définie pour tout réel $x > 0$ par : $g(x) = k\left(\dfrac{1 - x}{x}\right)$, où $k$ est un réel positif qui sera déterminé.
-
- Déterminer l'abscisse du point E.
- Déterminer la valeur du réel $k$, sachant que l'abscisse du point G est égale à $0,5$.
-
- Démontrer que la fonction $f$ admet pour primitive la fonction $F$ définie pour tout réel $x \geqslant 0$ par : \[F(x) = (x + 0,5) \times \ln (2x + 1) - x.\]
- Démontrer que $r = \dfrac{\text{e}}{2} - 1$.
- Déterminer une primitive $G$ de la fonction $g$ sur l'intervalle $]0~:~+ \infty[$.
- On admet que les résultats précédents permettent d'établir que $s = [\ln(2)]^2 + \dfrac{\ln (2) - 1}{2}$. La proposition B remplit-elle les conditions imposées par le fabricant?
- Vues: 46990
