Baccalauréat S Centres étrangers 10 juin 2015 - Exercice 2

Page 3 sur 10: Exercice 2

Exercice 2 4 points

Commun à tous les candidats

Pour chacune des quatre affirmations suivantes, indiquer si elle est vraie ou fausse en justifiant la réponse.
Il est attribué un point par réponse exacte correctement justifiée.
Une réponse non justifiée n'est pas prise en compte. Une absence de réponse n'est pas pénalisée.

1. Dans le plan muni d'un repère orthonormé, on note $S$ l'ensemble des points $M$ dont l'affixe $z$ vérifie les deux conditions : \[|z - 1| = |z - \text{i}|\quad \text{et} \quad |z - 3 - 2\text{i}| \leqslant 2.\]
   Sur la figure ci-contre, on a représenté le cercle de centre le point de coordonnées (3 ; 2) et de rayon 2, et la droite d'équation $y = x$. Cette droite coupe le cercle en deux points A et B.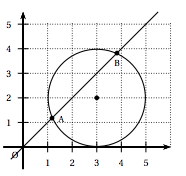
   
   
   1. Affirmation 1 : l'ensemble $S$ est le segment [AB].
   2. Affirmation 2 : le nombre complexe $\left(\sqrt{3} +\text{i}\right)^{ 1515 }$ est un réel.
   
   Pour les questions 3 et 4, on considère les points E (2 ; 1 ; - 3), F (1 ; -1 ; 2) et G (-1 ; 3 ; 1) dont les coordonnées sont définies dans un repère orthonormé de l'espace.
2. Affirmation 3 : une représentation paramétrique de la droite (EF) est donnée par: \[\left\{\begin{array}{l c r} x&=&2t\\ y&=&-3 + 4t\\ z&=&7-10t \end{array}\right., t\: \in \mathbb R.\]
3. Affirmation 4 : une mesure en degré de l'angle géométrique $\widehat{\text{FEG}}$, arrondie au degré, est 50°.