Suites, le cours
2.2.3. Technique par récurrence : pratique pour les suites du type $ u_{n+1} =f\left( u_n \right) $.
Exemple : Soit $\left( u_n \right) $ la suite définie par : $u_0=16$ et $u_{n+1}=\sqrt{u_n} $
Démontrons par récurrence que cette suite est décroissante.
On considère la propriété $(P)$ définie pour $n in \mathbb{N}$ par :$P(n) : 0\leq u_{n+1}\leq u_n$
· On a $u_1 = 4$ donc $0 \leq u_1 \leq u_0$, d'où $P(0)$. Donc $P$ est initialisée au rang 0.
· Montrons que $P$ est héréditaire à partir du rang 0.
Soit $n in \mathbb{N}$. Supposons $P(n) : 0\leq u_{n+1}\leq u_n$
Alors, par croissance de l'application $x\mapsto \sqrt x$ sur $\mathbb{R}^+$, nous avons :
$\sqrt 0\leq \sqrt{u_{n+1}}\leq \sqrt{u_n}$
d'où $ 0 \leq u_{n+2}\leq u_{n+1}$
D'où $P(n + 1)$.
La propriété $P$ est initialisée au rang 0 et héréditaire à partir du rang 0, donc d'après le principe de raisonnement par récurrence, elle est vraie à tout rang $n$:
pour tout $n\geq 0$, on a $u_{n+1} \leq u_n$
La suite $\left( u_n \right) $ est bien décroissante.
Une représentation graphique de cette suite:
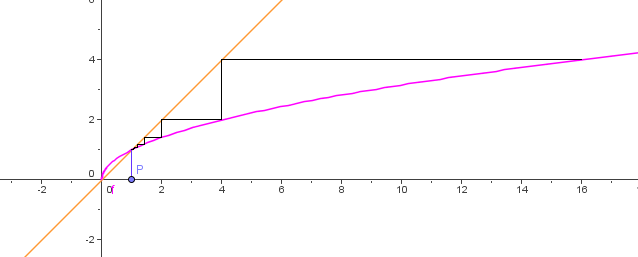
3. Suite majorée, suite minorée, suite bornée
3.1. Définition
Une suite $\left( u_n \right) $ est majorée lorsqu'il existe un réel $M$ tel que $u_n \leq M$ pour tout entier $n$.
Une suite $\left( u_n \right) $ est minorée lorsqu'il existe un réel $m$ tel que $u_n\geq m$ pour tout entier $n$.
Une suite $\left( u_n \right) $ est bornée lorsqu'elle est minorée et majorée :
il existe des réels $m$ et $M$ tels que $m \leq u_n \leq M$ pour tout entier $n$.
Remarque :
Une suite $\left( u_n \right) $ est bornée si et seulement si il existe un réel $M$ tel que $|un| \leq M$ pour tout entier $n$.
En effet, si $\left( u_n \right) $ est bornée, il existe des réels $a$ et $b$ tels que pour tout entier $n$ on ait :
$a \leq u_n \leq b$
Notons $M = max(|a| ; |b|)$. Comme $b \leq |b| \leq M$ et $-M \leq -|a| \leq a$, on obtient :
$-M \leq u_n \leq M$
D'où : $|u_n| \leq M$
La réciproque est évidente.
3.2. Techniques pour prouver qu'une suite est majorée (ou minorée ou bornée)
3.2.1. Technique algébrique : manipulation d'inégalités
Exemple 1 : $u_n =\dfrac{(-1)^n + \sin n }{n^2}$ , pour $n \in \mathbb{N}^{\star}$.
On a : $ -1\leq \sin n \leq 1$ et $-1\leq \sin n \leq 1$ donc en ajoutant membre à membre ces deux inégalités de même sens, il vient:$-2 \leq (-1)^n + \sin n \leq 2 $ et $0 \leq \dfrac{1}{n}^2\leq 1$
D'où : $-2 \leq u_n \leq 2$
La suite $\left( u_n \right) $ est bornée.
Exemple 2 : $u_n = \displaystyle\sum_{k=1} ^ n \dfrac{1}{k^2} $ , pour $n \in \mathbb{N}^{\star}$
Montrer que $\left( u_n \right) $ est majorée par 2.
En remarquant que, pour $k\geq 2 : \dfrac{1}{k^2}\leq \dfrac{1}{k(k-1)}\leq \dfrac{1}{k-1}- \dfrac{1}{k}$.
On a : $u_n = 1 +\dfrac{1}{2}^2+\dfrac{1}{3}^2+........+\dfrac{1}{n}^2$
On écrit successivement: en remplaçant $k$ par :$2;3; .......;n-1;n$ dans la relation $(R) : \dfrac{1}{k^2}\leq \dfrac{1}{k-1}- \dfrac{1}{k}$.
| $k=2$ | donne | $\dfrac{1}{2} ^2\leq 1 - \dfrac{1}{2}$ |
| $k=3$ | donne | $\dfrac{1}{3} ^2\leq \dfrac{1}{2} - \dfrac{1}{3}$ |
| $k=4$ | donne | $\dfrac{1}{4} ^2\leq \dfrac{1}{3} - \dfrac{1}{4}$ |
| $k=n-1$ | donne | $\dfrac{1}{(n-1) ^2} \leq \dfrac{1}{n-2} - \dfrac{1}{n-1}$ |
| $k=n$ | donne | $\dfrac{1}{n ^2} \leq \dfrac{1}{n-1} - \dfrac{1}{n-2}$ |
On ajoute ces $n-1$ inégalités, d'où $ \dfrac{1}{2}^2+\dfrac{1}{3}^2+........+\dfrac{1}{n}^2\leq 1-\dfrac{1}{n}$
Puis $1+ \dfrac{1}{2}^2+\dfrac{1}{3}^2+........+\dfrac{1}{n}^2\leq 2-\dfrac{1}{n}$ ;
Soit $u_n\leq 2$
On a ainsi prouvé que $\left( u_n \right)$est majorée par $2$.
Exemple 3 :Soit $\left( u_n \right) $la suite définie par:$u_n = \displaystyle\sum_{k=0} ^ n \dfrac{1}{k!} $
Montrer que $\left( u_n \right) $ est majorée par 3.
Montrons tout d'abord, par récurrence, la propriété $P$, définie pour $k \in \mathbb{N}^{\star}$, par :
$P(k) : k!\geq 2^{k -1}$
· On a évidemment $P(1)$, en effet $1!=1$ et $2^{1 -1}=1$. La propriété $P$ est initialisée au rang 1.
· Montrons que $P$ est héréditaire à partir du rang 1.
Soit $k \in N^{\star}$. Supposons $P(k) : k!\geq 2^{k -1}$
Alors on a : $(k + 1)! = (k + 1) \times k!\geq (k + 1) \times 2^{k -1}$
Et comme $k\geq 1$on déduit $(k + 1)\geq 2$ : puis $(k + 1)!\geq 2^ k$, Ce qui est $P(k + 1)$.
Du principe de raisonnement par récurrence, on déduit :
$k!\geq 2^{k -1} $ pour tout $k\geq 1$.
On peut donc écrire : $u_n = 1 + sum_{k=1}^n \dfrac{1}{k!}$.
D'après la propriété établie par récurrence, on a pour tout $k\geq 1$: $k!\geq 2^{k -1} $;
en prenant les inverses il vient pour tout $k\geq 1$ $(Q) : \dfrac{1}{k!}\leq (\dfrac{1}{2})^(k-1)$.
On écrit successivement: en remplaçant $k$ par :$1;2;3; .......;n-1;n$ dans la relation $(Q)$ :
| $k=1$ | donne | $\dfrac{1}{1!} \leq \left(\dfrac{1}{2}\right)^0$ |
| $k=2$ | donne | $\dfrac{1}{2!} \leq \left(\dfrac{1}{2}\right)^1$ |
| $k=3$ | donne | $\dfrac{1}{3!} \leq \left(\dfrac{1}{2}\right)^2$ |
| $k=n-1$ | donne | $\dfrac{1}{(n-1) !} \leq \left(\dfrac{1}{2}\right)^{n-2}$ |
| $k=n$ | donne | $\dfrac{1}{n !}\leq \left(\dfrac{1}{2} \right)^{n-1}$ |
On ajoute membre à membre ces $n$ inégalités, d'où $ \dfrac{1}{1!}+\dfrac{1}{2!}+\dfrac{1}{3!}+........+\dfrac{1}{n!}\leq 1+\left (\dfrac{1}{2}\right)+\left (\dfrac{1}{2}\right)^2+.....+\left(\dfrac{1}{2} \right)^{n-1}$
On reconnaît une somme de $n$ termes consécutifs d'une suite géométrique de raison $\dfrac{1}{2}$, d'où :
D'après le cours : Si $q\neq 1$alors $1+q+q^ 2+q^3+........+q^n=\dfrac{1- \text{ raison } ^ {\text{ Nombre de termes}}}{1- \text{ raison }} \times\text{ premier terme} $.
Ici $ 1+\left (\dfrac{1}{2}\right)+\left (\dfrac{1}{2}\right)^2+.....+\left(\dfrac{1}{2} \right)^{n-1}=\dfrac{1-\left(\dfrac{1}{2}\right )^n}{1-\dfrac{1}{2}} \times 1=2 \times\left(1-(\dfrac{1}{2})^n\right)$
On a donc $ \dfrac{1}{1!}+\dfrac{1}{2!}+\dfrac{1}{3!}+........+\dfrac{1}{n!}\leq 2 \times(1-(\dfrac{1}{2})^n)$
On ajoute $1$: $ 1+\dfrac{1}{1!}+\dfrac{1}{2!}+\dfrac{1}{3!}+........+\dfrac{1}{n!}\leq 3-2 \times(\dfrac{1}{2})^n$
On a ainsi établi que pour tout $ n \in \mathbb{N}$ on a $u_n\leq 3$.
3.2.2. Technique fonctionnelle
Exemple : $u_n = \dfrac{2 n^2+1}{n^2+5}$
Considérons la fonction $f$ définie sur $[0 ; +\infty[$ par : $f(x)=\dfrac{2 x^2+1}{x^2+5}$
On a déjà vu, plus haut, que $f$ est croissante sur $[0 ; +\infty[$.
Par ailleurs, on a $f(0) = \dfrac{1}{5}$ et$\lim\limits_{x \to +\infty}f(x)=2$.
On duit donc que pour tout $x \in [0;+\infty[$ on a $\dfrac{1}{5}\leq f(x)\leq 2$;
et donc en particulier pour tout $n \in \mathbb{N}$ on a : $\dfrac{1}{5}\leq f(n)\leq 2$ ce qui fournit $\dfrac{1}{5}\leq u_n\leq 2$
La suite $\left( u_n \right) $ est donc bornée : majorée par $2$ et minorée par $\dfrac{1}{5}$
3.3.3. Technique par récurrence
Exemple : $u_{n+1} = \sqrt{6 + u_n}$ avec $u_0 = 0$
On considère la propriété $P$, définie pour $n \in \mathbb{N}$, par :
$P(n) : 0 \leq u_n \leq 3$
· Par hypothèse, on a $P(0)$; en effet $0\leq u_0\leq 3$. La propriété est initialisée au rang 0.
· Montrons que $P$ est héréditaire à partir du rang 0.
Soit $nin \mathbb{N}$. Supposons $P(n)$ : $0 \leq un\leq 3$
Alors, en ajoutant 6 :$ 6 \leq 6 + u_n \leq 9$
Par passage à la racine carrée (qui est une fonction croissante sur $\mathbb{R}^{+}$) :
$\sqrt6\leq \sqrt{ 6 + u_n}\leq 3$
Donc :$0 \leq u_{n+1}\leq 3$
Conclusion : pour tout entier $n\geq 0$ , on a : $0 \leq u_n \leq 3$
On peut aussi retrouver ce résultat par la méthode algébrique. (Manipulation d'inégalités)
- Vues: 39690
