Suites, le cours
4.2. Propriété Unicité de la limite
Si $\left( u_n \right) $ converge, alors sa limite $l$ est unique.
Démonstration
Raisonnons par l'absurde. Supposons que la suite $\left( u_n \right) $ admette deux limites distinctes $l_1$ et $l_2$ avec $l_1 < l_2$.
Notons $d = l_2 - l_1$.
Comme $\left( u_n \right) $ converge vers $l_1$, à partir d'un certain rang $N_1$, tous les termes de la suite sont dans l'intervalle ouvert $I_1$ de centre $l_1$ et de rayon $\dfrac{d}{3}$ .
De même, comme $\left( u_n \right) $ converge vers $l_2$, à partir d'un certain rang $N_2$, tous les termes de la suite sont dans l'intervalle ouvert $I_2$ de centre $l_2$ et de rayon $\dfrac{d}{3}$ .
Donc à partir du rang $N = max(N_1, N_2)$, tous les termes de la suite sont simultanément dans $I_1$ et $I_2$. Or ces deux
intervalles sont disjoints (ils ne se chevauchent pas). Ce qui n'est pas possible.
Ceci prouve l'unicité de la limite.
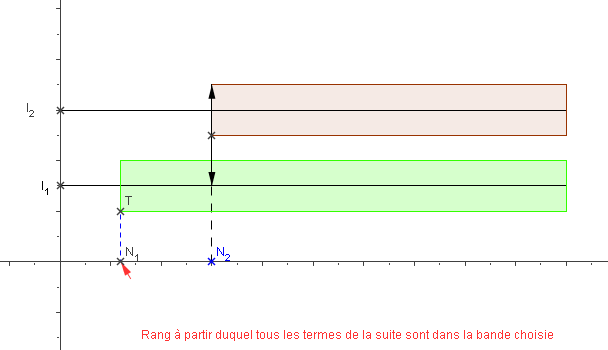
Illustration : Comment, à partir du rang $N_1$, tous les termes de la suite pourraient-ils se situer dans ces deux "tuyaux" ?
- Vues: 39867
